In the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC
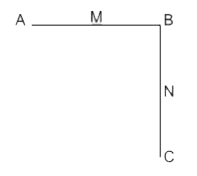
Step by step video & image solution for In the give figure AB = BC, M is the mid point of AB and N is the mid point of BC, Show that AM = NC by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - PRACTICE TEST8videos
INTRODUCTION TO EUCLID'S GEOMETRY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - INTRODUCTION TO EUCLID'S GEOMETRYEXERCISE - PART -B9videos
INTRODUCTION TO EUCLID'S GEOMETRY
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - HERON'S FORMULAEXERCISE - PRACTICE TEST8videos
HERON'S FORMULA
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - PRACTICE TEST12videos
LINEAR EQUATIONS IN TWO VARIABLES
Similar Questions
In the adjoining figure
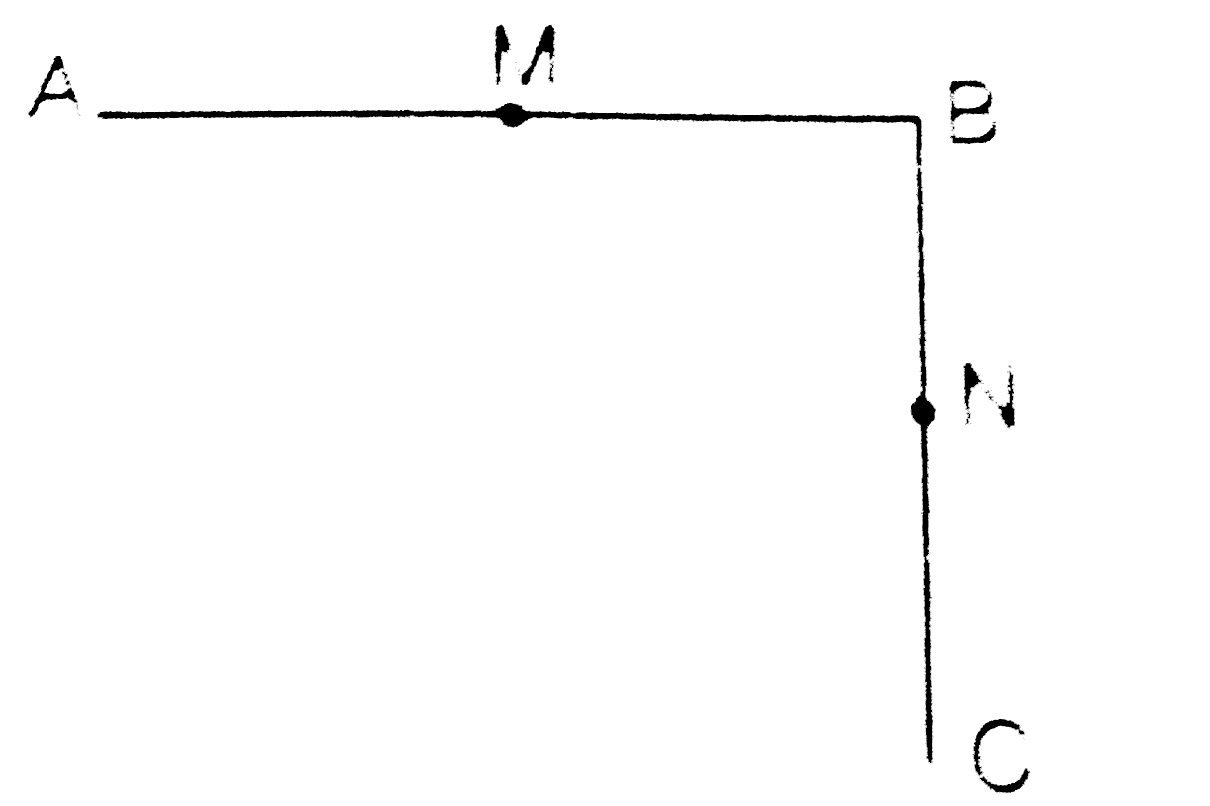
(i) AB=BC, M is the mid -point of AB and N is the mid- point of BC. Show that AM=NC.
(ii) BM=BN,M is the mid- point of AB and N is the mid - point of BC. Show that AB=BC.View Solutionin figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View Solution
Knowledge Check
- Question 1 - Select One
Locus of mid point of AB is
Ax2=−2yB2x2=−yCx2=−4yDx22−y21=−1 - Question 2 - Select One
If ABCD is a square, X is the mid point of AB and Y is the mid point of BC, then which of the following is NOT correct?
AThe triangles ADX and BAY are congruentB∠DXA=∠AYBC∠ADX=∠BAYDDX is not perpendicular to AY
in figure , M is the mid-point of AB and N is the mid-point of BC (1) if AB=BC , prove that AM=NC
View SolutionIn the figure, M is the mid - point of [AB] and N is the mid - point of [CD] and O is the mid - point of [MN]. Prove that :
(i) −−→OA+−−→OB+−−→OC+−−→OD=→0
(ii) −−→BC+−−→AD=2−−−→MN.
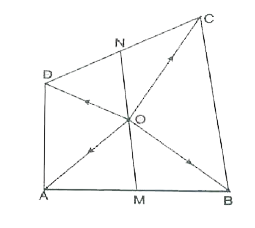 View Solution
View SolutionIn the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of ΔBOEandΔABC
 View Solution
View SolutionIn the given figure, P is the mid-point of arc APB and M is the mid-int of chord AB of a circle with centre O. Prove that PM⊥AB
View SolutionIn the given figure, in △ABC, D is the mid-point cf AB and P is any point on BC. If CQ∣∣PD meets AB in Q and area of △ABC=30cm2, then, area of △BPQ is
View SolutionWe have AC=XD , C is the mid point of AB and D is the mid point of XY, Using Euclid's axiom ,show that AB=XY
View Solution

