In the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
Area of the shaded region = Area of the square -4 times Area of the sector of the circle
area of a circle =(2×2)−4×14(π)(1)2=4−π
Required probability=AreaofshadedregionAreaof□=4−π4
Topper's Solved these Questions
Similar Questions
In figure, a dart is thrown and lands n the interior of the circle. What is the probability that the dart will land in the shaded region?
View Solution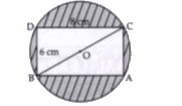
In figure, a dart is thrown and lands in the interior of the circle.
What is the probability that the dart will land in the shaded region ?
View Solution
Knowledge Check
A point is selected randomly from the interior of a circle. The probability that the point is closer to the centre, then the boundary of circle is
A34B14C12D23
In the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View SolutionIn the adjoining figure a dart is thrown at the dart board and lands in the interior of the circle . What is the probability that the dart will land in the shaded region.
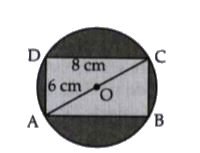
View SolutionA point is selected at random from the interior of a circle. The probability that the point is closer to the centre than the boundary of the circle is
View Solution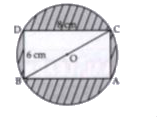
In figure, a dart is thrown and lands in the interior of the circle.
What is the probability that the dart will land in rectangle ABCD region ?
View SolutionIn the given figure OABC is a quadrant of a circle with centre O and radius 3.5cm.If OD=2cm,find the area of the shaded region.
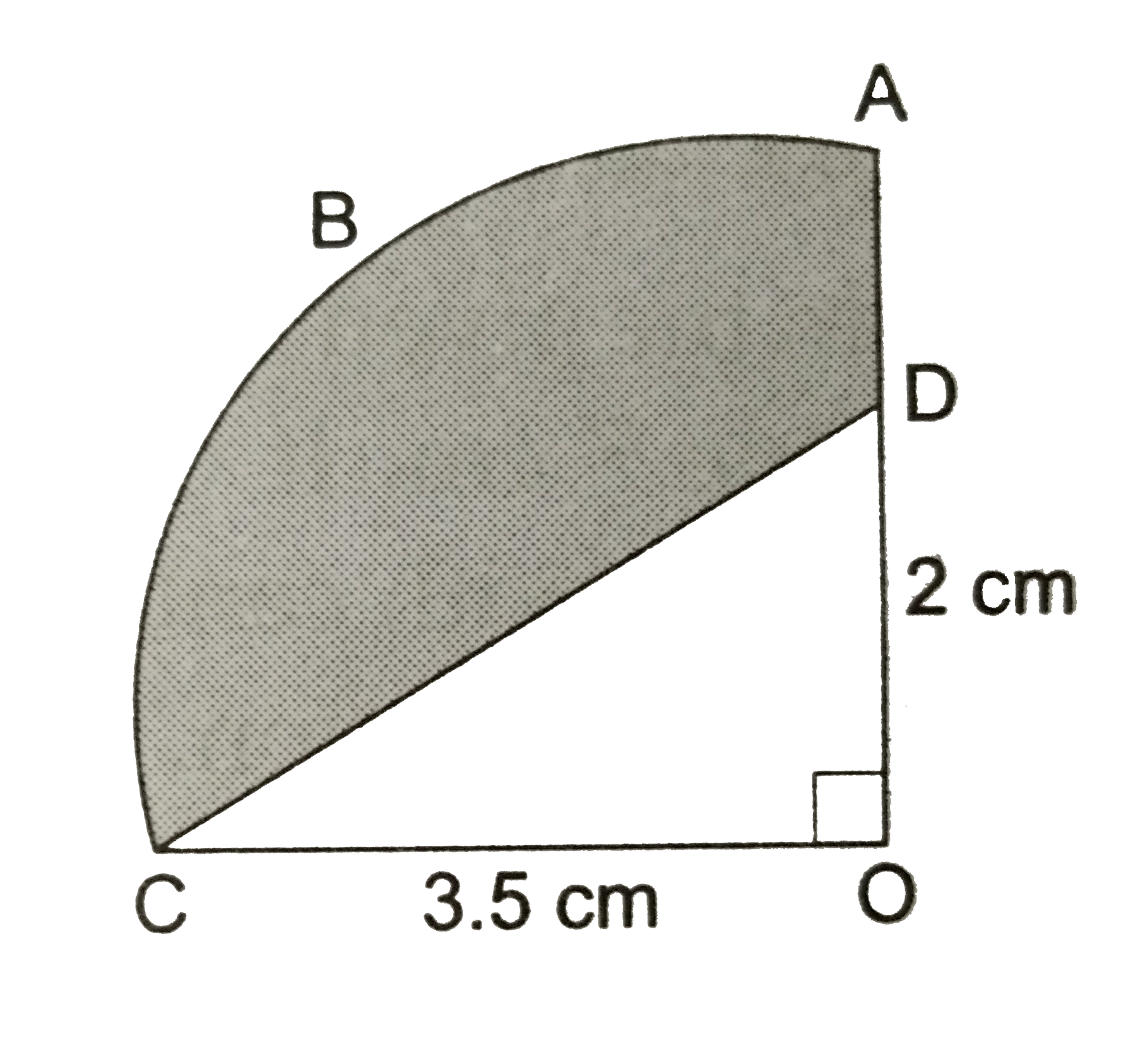
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.

View SolutionIn the given figure, ABCD is a square of side 7cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.
View Solution
