In the given figure, A, B, C and D are centres of four circles that have a radius of 1 unit. If a point is selected at random from interior of square ABCD, then what is the probability that it lies in the shaded region
To solve the problem, we need to find the probability that a randomly selected point from the interior of square ABCD lies in the shaded region formed by the circles centered at points A, B, C, and D.
1. Identify the Dimensions of the Square:
- The centers of the circles A, B, C, and D are at the corners of the square.
- Each circle has a radius of 1 unit.
- Therefore, the side length of the square ABCD is the distance between two adjacent centers (which is 1 unit) plus the diameters of the circles (which is 2 units). Thus, the side length of the square is:
Side length=1+1=2 units
2. Calculate the Area of the Square:
- The area of the square is given by the formula:
Area of square=side2=22=4 square units
3. Calculate the Area of One Circle:
- The area of one circle is calculated using the formula:
Area of circle=πr2
- Substituting the radius r=1:
Area of one circle=π×12=π square units
4. Calculate the Area of the Four Circles:
- Since there are four circles, the total area of the circles is:
Total area of circles=4×Area of one circle=4×π=4π square units
5. Calculate the Area of the Shaded Region:
- The shaded region is the area of the square minus the area covered by the circles. However, since the circles overlap, we need to consider only the area of the square minus the area of the sectors formed by the circles at the corners.
- Each circle contributes a quarter of its area to the shaded region, so the area of the sectors is:
Area of sectors=4×(14×Area of one circle)=4×(14×π)=π square units
- Thus, the area of the shaded region is:
Area of shaded region=Area of square−Area of sectors=4−π square units
6. Calculate the Probability:
- The probability that a randomly selected point lies in the shaded region is given by the ratio of the area of the shaded region to the area of the square:
Probability=Area of shaded regionArea of square=4−π4
Final Answer:
The probability that a point lies in the shaded region is:
4−π4
- The centers of the circles A, B, C, and D are at the corners of the square.
- Each circle has a radius of 1 unit.
- Therefore, the side length of the square ABCD is the distance between two adjacent centers (which is 1 unit) plus the diameters of the circles (which is 2 units). Thus, the side length of the square is:
Side length=1+1=2 units
- The area of the square is given by the formula:
Area of square=side2=22=4 square units
- The area of one circle is calculated using the formula:
Area of circle=πr2
- Substituting the radius r=1:
Area of one circle=π×12=π square units
- Since there are four circles, the total area of the circles is:
Total area of circles=4×Area of one circle=4×π=4π square units
- The shaded region is the area of the square minus the area covered by the circles. However, since the circles overlap, we need to consider only the area of the square minus the area of the sectors formed by the circles at the corners.
- Each circle contributes a quarter of its area to the shaded region, so the area of the sectors is:
Area of sectors=4×(14×Area of one circle)=4×(14×π)=π square units
- Thus, the area of the shaded region is:
Area of shaded region=Area of square−Area of sectors=4−π square units
- The probability that a randomly selected point lies in the shaded region is given by the ratio of the area of the shaded region to the area of the square:
Probability=Area of shaded regionArea of square=4−π4
The probability that a point lies in the shaded region is:
4−π4
Topper's Solved these Questions
Similar Questions
In figure, a dart is thrown and lands in the interior of the circle. What is the probability that the dart will land in the shaded region?
View SolutionIn the Fig. 13.12, JKLM is a square with sides of length 6 units. Points A and B are the mid-points of sides KL and LM respectively. If a point is selected at random from the interior of the square. What is the probability that the point will be chosen from the interior of JAB ? (FIGURE)
View SolutionIn the figure, the smaller square has sides of length 2 and the larger square has sides of length 4. If a point is chosen at random from the larger square, what is the probability that it will be from the small square?
 View Solution
View SolutionThe triangles inside △ABC , shown above, are formed by joining the midpoints of the sides and then repeating the process. If a point is chosen at random inside △ABC ,what is the probability that the point lies in the shaded region ?
View SolutionSuppose we have four boxes A,B,C and D containing coloured marbles as given below :One of the boxes has been selected at random and a single marble is drawn from it. If the marble is red, what is the probability that it was drawn from box A? box B?, box C?
View Solution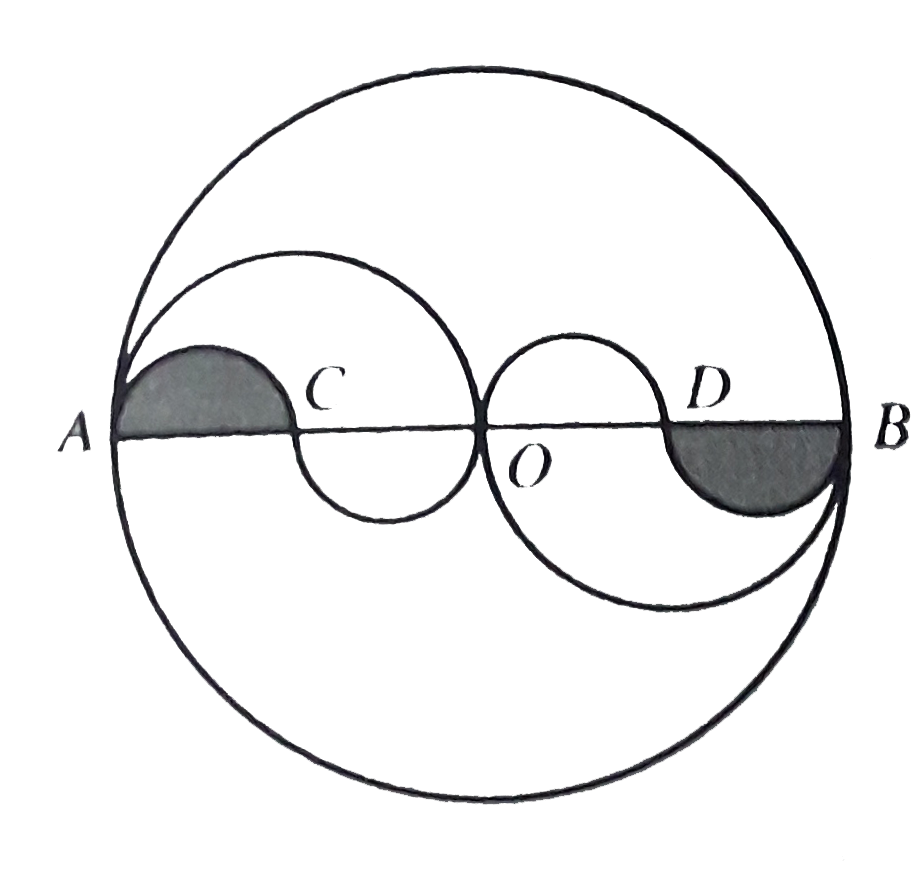
In the circle shown above, O is the center and ¯¯¯¯¯¯AB is a diameter . There are two semicircles with diameters ¯¯¯¯¯¯AO and ¯¯¯¯¯¯BO , and four smaller semicircles with congruent diameters ¯¯¯¯¯¯AC,¯¯¯¯¯¯CO,¯¯¯¯¯¯OD and ¯¯¯¯¯¯DB . A point is picked at random in the large circle . What is the probability that it lands in a shaded region ?View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.
 View Solution
View Solution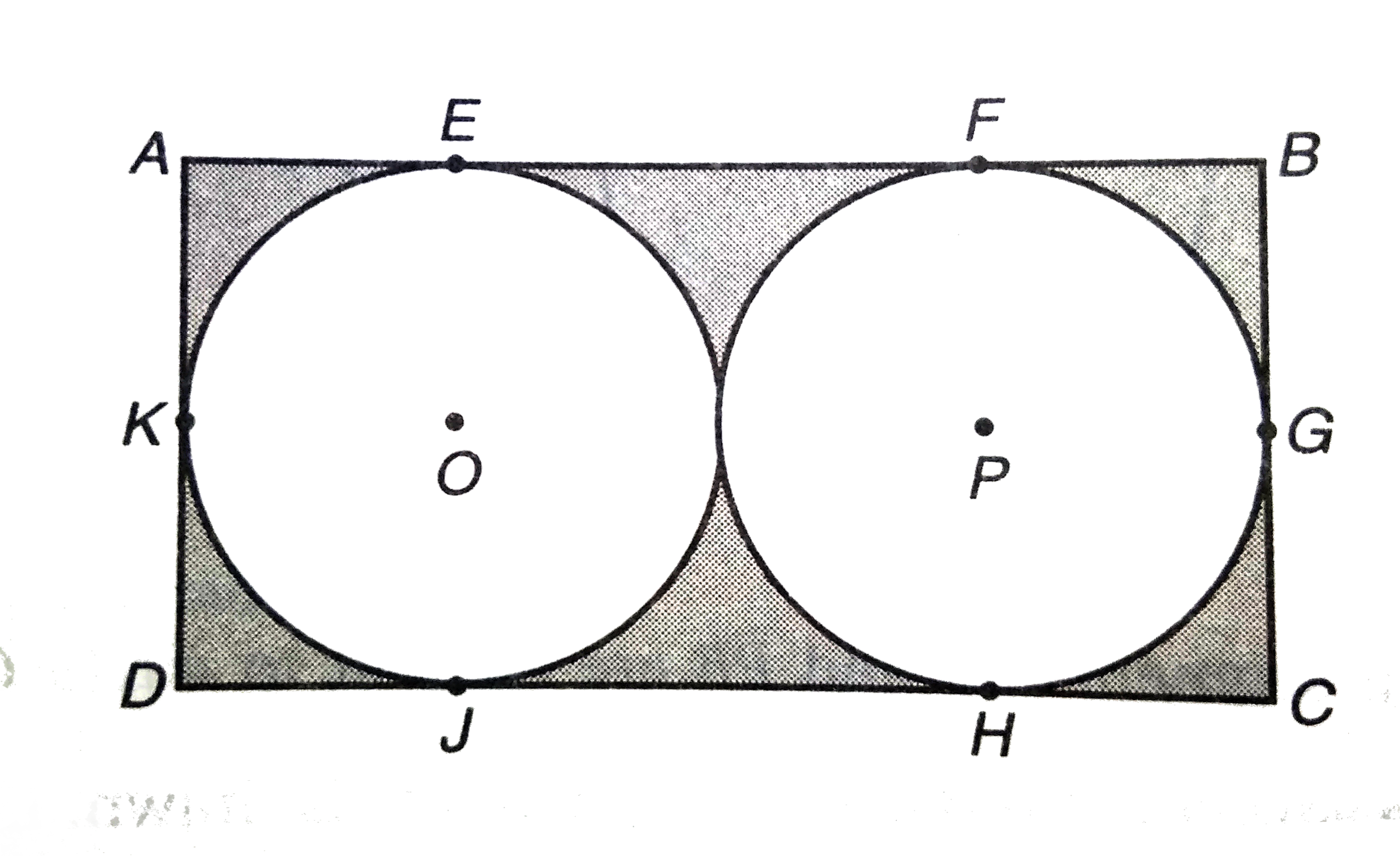
In the figure above, the radius of each circle is 1. If circles O and P touch the sides of rectangle ABCD only at the lettered points, what is the area of the shaded region?View SolutionIn the given figure, ABCD is a square of side 7 cm. DPBA and DQBC are quardrants of circles each of the radius 7 cm. Find the area of the shaded region.
 View Solution
View SolutionA point is selected at random from inside a circle. The probability that the point is closer to the circumference of the circle than to its centre, is
View Solution

