In the given figure, AB and CD are two chords of a circle, intersecting each other at a point E . Prove that
∠AEC=12( angle subtended by arc CXA, at the centre + angle subtended by arc DYB at the centre).
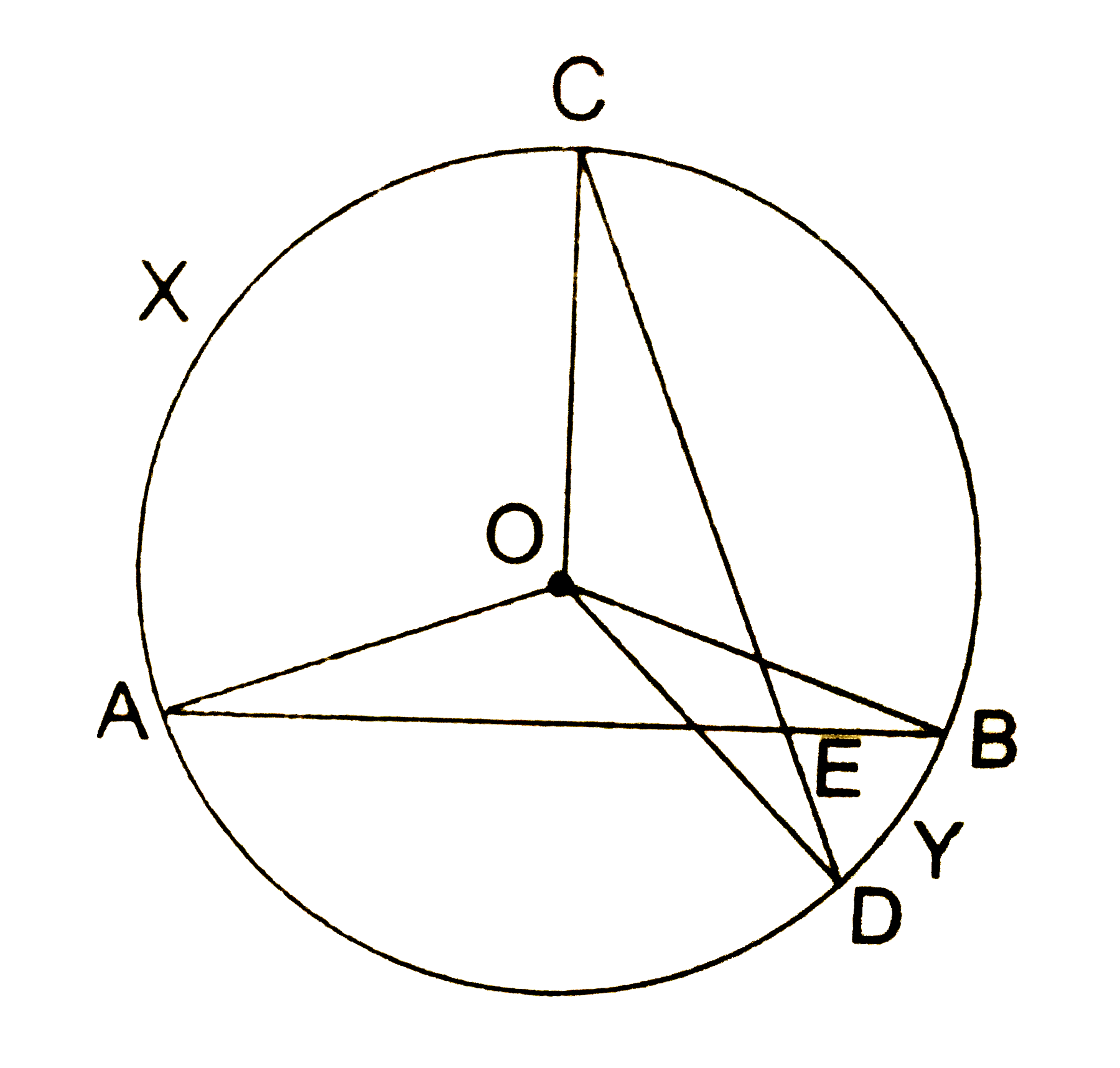
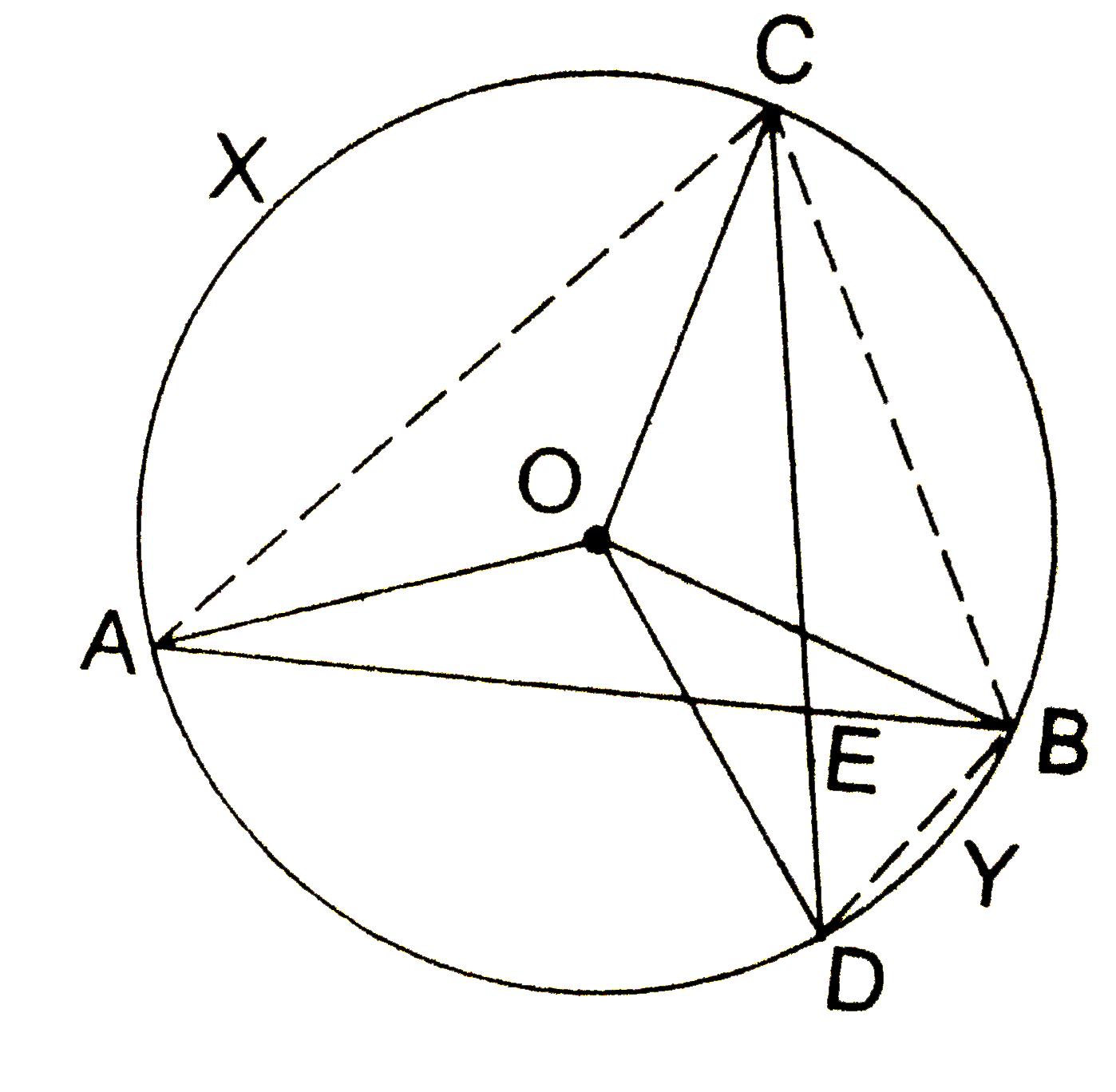
Join AC, BC and BD
Since AC is a chord , we have
∠AOC=2∠ABC ...(i)
Similarly , ∠DOB=2∠DCB. ....(ii)
∴∠AOC+∠DOB=2(∠ABC+∠DCB)=2∠AEC.
Hence, ∠AEC=12(∠AOC+∠DOB)
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
In the figure, AB and CD are two chords of a circle, interacting each other at a point E. Prove that ∠AEC = 1/2(angle subtended by arc CXA. at the centre + angle subtended by arc DYB at the centre).
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View Solution
Knowledge Check
Which of the following can be the angle subtended by a minor arc at the centre?
A100∘B220∘C180∘D270∘A, B and C are the three points on a circle such that ∠ABC=35∘and∠BAC=85∘. What is the angle (in degrees) subtended by arc AB at the centre of the circle?
A60B90C135D120If 76 is divided into four parts proportional to 7, 5, 3, 4, then the smallest part is:
AA) 12BB) 15CB) 15DD) 19
If the angle subtended by two chords of a circle at the centre are equal; the chords are equal.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionTheorem 10.8 : The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, the chords are equal.
View SolutionFind the angle subtended at the centre of a circle of radius 'a' by an arc of length (aπ/4) .
View Solution
