In the given figure, ABCD is a quadrilateral and E and F are points on AD and CD respectively such that AB = CB, ∠ABE=∠CBFand∠EBD=∠FBD. Prove that BE=BF.
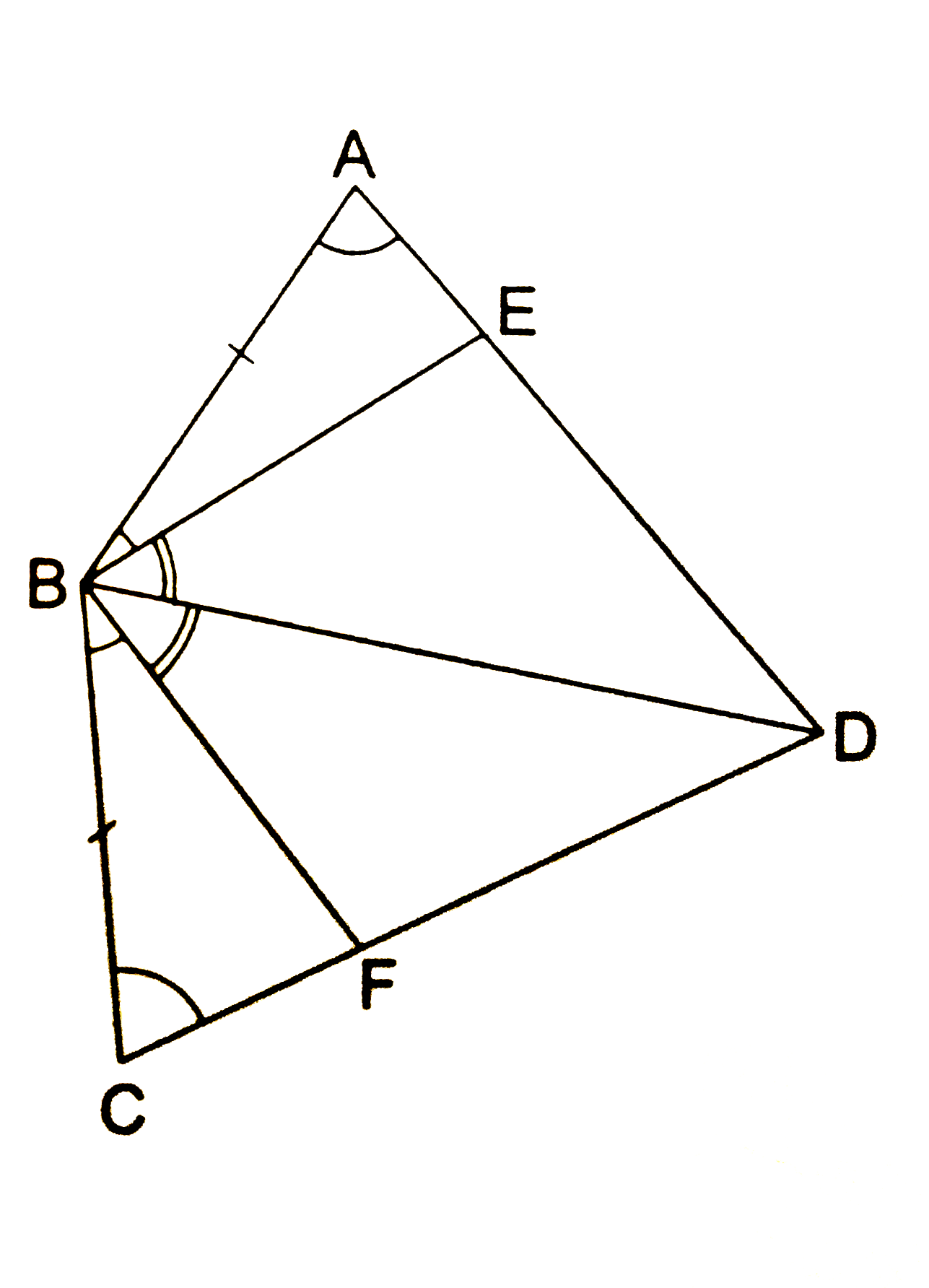
∠ABE=∠CBFand∠EBD=∠FBD
⇒ ∠ABE+∠EBD=∠CBF+∠FBD
⇒ ∠ABD+∠CBD. …(i)
Now, in ΔABDandΔCBD, we have
AB=CB (given)
∠ABD=∠CBD [from (i)]
BD=BD (common)
∴ ΔABD≅ΔCBD [SAS-criteria].
∴ ∠BAD=∠BCD [c.p.c.t.]
⇒ ∠BAE=∠BCF. ...(ii)
Now, in ΔABEandΔCBF, we have
AB=CB (given)
∠ABE=∠CBF (given)
∠BAE=∠BCF [proved in (ii)]
∴ ΔABE≅ΔCBF [AAS-criteria].
Hence, BE = BF.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
In the adjoining figure, ABCD is a quadrilateral. M and N are the points on AD and CD respectively such that AB=BC,∠ABM=∠CBN and ∠MBD=∠NBD. Prove that BM=BN.

View SolutionIn the given figure, ABCD is a parallelogram. E and F are any two points on AB and BC, respectively. Prove that ar(△ADF)=ar(△DCE).
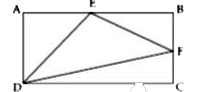
View SolutionIn the given figure ABCD is a parallelogram in which AB||CD and E and F are the mid points of AB and BC respectively. What is the area of ∠BEF?
View SolutionIf ABCD is quadrilateral and EandF are the mid-points of ACandBD respectively, prove that →AB+→AD +→CB +→CD =4 →EF.
View SolutionThe figure ABCD is a quadrilateral in which AB = CD and BC = AD. Its area is
View SolutionIn the given figure ABCD is, ABCD is a quadrilateral in which AB∣∣DC and AD∣∣BC prove that ANGLEADC=ANGLEABC.

View SolutionAB is a line and P is its midpoint. D and E are two points on the same side of line segment AB such that ∠BAD=∠ABEand∠EPA=∠DPB. Prove that
AD=BE
View SolutionABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:

View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
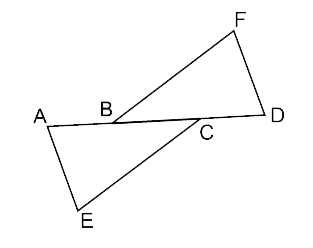
View SolutionIn the given figure , AB=CD,CE=BF and ∠ACE==∠DBF . Prove that
AE=DF
View Solution
