In the given figure, ABCD is a square and ∠PQR=90∘.IfPB=QC=DR, prove that.
(i) QB = RC
(ii) PQ = QR
(iii) ∠QPR=45∘
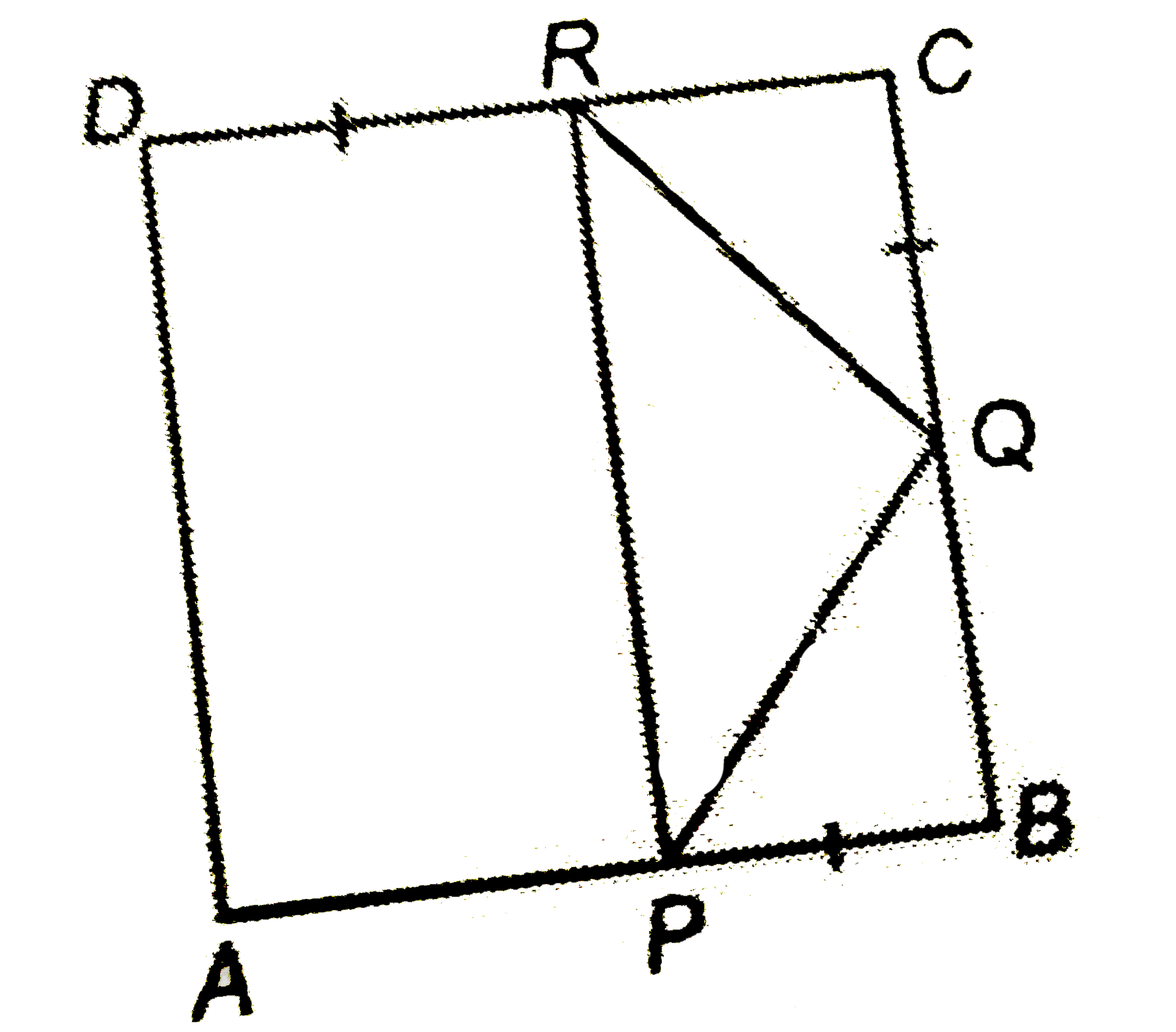
Step by step video & image solution for In the given figure, ABCD is a square and anglePQR=90^(@).If PB=QC=DR, prove that. (i) QB = RC (ii) PQ = QR (iii) angleQPR=45^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In the given figure , DEFG is a square and ∠BAC=90∘ prove that (i) △AGF~△DBG (ii)△AGF~△EFC
View SolutionIn the given figure, ∠SPR=∠QRP and ∠RSP=∠PQR. Prove that :
(i) PQ=RS
(ii) PS=QR

View SolutionIn the given figure, QR is parallel to AB and DR is parallel to QB.
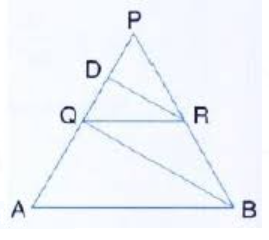
Prove that : PQ2=PD×PA.
View SolutionIn the given figure, we have PQ=SR and PR=SQ. Prove that :
(i) ΔPQR≅ΔSRQ
(ii) ∠PQR=∠SRQ
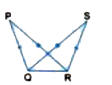
View SolutionIn the given figure, ∠PQR=∠PST=90∘, PQ = 5cm and PS = 2 cm.
Prove that △PQR ~△PST

View SolutionIn the adjoining figure, ABCD is a square and PAB is an equilateral triangle. Find :
(i) ∠APD
(ii) ∠PDC
(iii) ∠DPC
(iv) Prove that DP=CP

View SolutionIn the given figure, AD = DB = DE ∠EAC=∠FACand∠F=90∘
Prove that
(i) ∠AEB=90∘
(ii) ΔCEG is isosceles.
(iii) ∠CEG=∠EAF
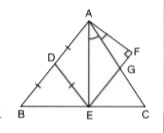
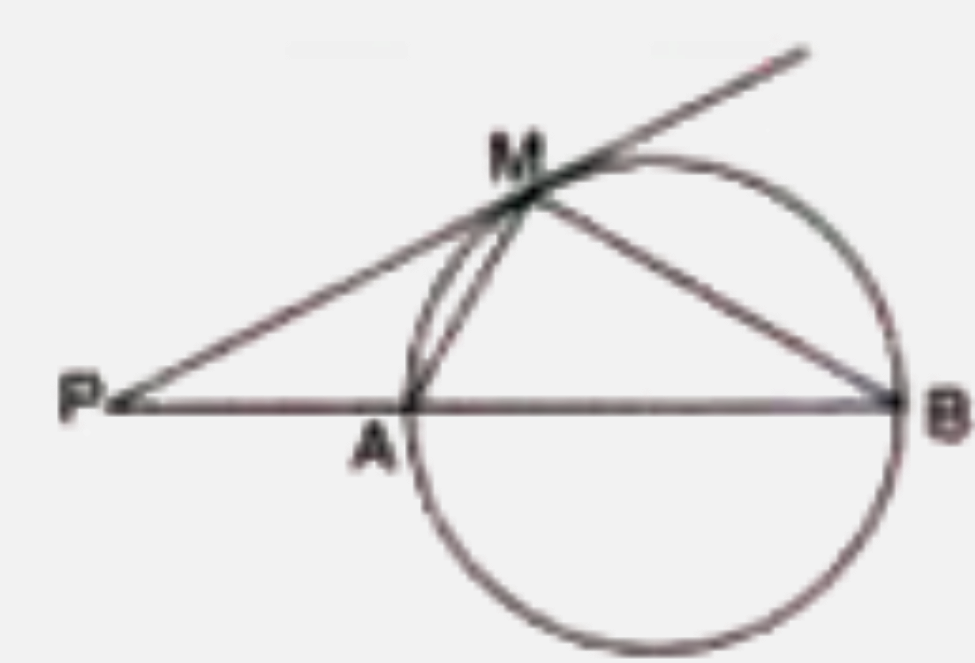
View SolutionIn the given figure PM is a tangent to the circle and PA =AM.
Prove that
(i) ΔPMB is isosceles
(ii) PAXxPB=MB2
View SolutionIn the given figure, AB⊥BD,CD⊥BD and AB=CD. Prove that :
(i) ΔABD≅ΔCDB
(ii) AD-CB

View SolutionIn the following figure, OA = OC and AB = BC. Prove that :
(i) ∠AOB=90∘
(ii) ΔAOD≅ΔCOD
(iii) AD = CD

View Solution
