In a square ABCD, diagonals meet at O. P is point on BC such that OB = BP.Show that (i) ∠POC=(2212)∘
(ii) ∠BDC=2∠POC
(iii) ∠BOP=3∠COP
To solve the given problem, we will break it down into three parts as requested.
Given:
- A square ABCD with diagonals AC and BD intersecting at point O.
- Point P is on side BC such that OB = BP.
To Prove:
1. ∠POC=2212∘
2. ∠BDC=2∠POC
3. ∠BOP=3∠COP
1. Identify the Angles:
- Since ABCD is a square, each angle is 90∘.
- The diagonals bisect each other at O and intersect at 90∘.
2. Triangle BOP:
- In triangle BOP, since OB = BP, it is an isosceles triangle.
- Let ∠BOP=∠BPO=x.
3. Using Angle Sum Property:
- The sum of angles in triangle BOP is:
∠OBP+∠BOP+∠BPO=180∘
- We know ∠OBP=45∘ (since it is half of 90∘).
- Thus,
45∘+x+x=180∘
2x=180∘−45∘=135∘
x=67.5∘
4. Finding ∠POC:
- Since diagonals bisect each other at O:
∠BOP+∠POC=90∘
- Therefore,
67.5∘+∠POC=90∘
∠POC=90∘−67.5∘=22.5∘=2212∘
Part (ii): Prove ∠BDC=2∠POC
1. Finding ∠BDC:
- In square ABCD, ∠BDC=45∘ because the diagonal divides the angle ∠ADC=90∘ into two equal parts.
2. Using ∠POC:
- We already found ∠POC=22.5∘.
- Therefore,
2∠POC=2×22.5∘=45∘
- Thus, ∠BDC=2∠POC.
Part (iii): Prove ∠BOP=3∠COP
1. Finding ∠COP:
- Since ∠POC=22.5∘ and ∠COP=∠POC (as they are the same angle),
∠COP=22.5∘
2. Using ∠BOP:
- We already found ∠BOP=67.5∘.
- Now, check if ∠BOP=3∠COP:
3×∠COP=3×22.5∘=67.5∘
- Thus, ∠BOP=3∠COP.
Conclusion:
All parts of the problem have been proved successfully.
- A square ABCD with diagonals AC and BD intersecting at point O.
- Point P is on side BC such that OB = BP.
1. ∠POC=2212∘
2. ∠BDC=2∠POC
3. ∠BOP=3∠COP
- Since ABCD is a square, each angle is 90∘.
- The diagonals bisect each other at O and intersect at 90∘.
- In triangle BOP, since OB = BP, it is an isosceles triangle.
- Let ∠BOP=∠BPO=x.
- The sum of angles in triangle BOP is:
∠OBP+∠BOP+∠BPO=180∘
- We know ∠OBP=45∘ (since it is half of 90∘).
- Thus,
45∘+x+x=180∘
2x=180∘−45∘=135∘
x=67.5∘
- Since diagonals bisect each other at O:
∠BOP+∠POC=90∘
- Therefore,
67.5∘+∠POC=90∘
∠POC=90∘−67.5∘=22.5∘=2212∘
- In square ABCD, ∠BDC=45∘ because the diagonal divides the angle ∠ADC=90∘ into two equal parts.
- We already found ∠POC=22.5∘.
- Therefore,
2∠POC=2×22.5∘=45∘
- Thus, ∠BDC=2∠POC.
- Since ∠POC=22.5∘ and ∠COP=∠POC (as they are the same angle),
∠COP=22.5∘
- We already found ∠BOP=67.5∘.
- Now, check if ∠BOP=3∠COP:
3×∠COP=3×22.5∘=67.5∘
- Thus, ∠BOP=3∠COP.
All parts of the problem have been proved successfully.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Exercise 8b
15 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
Similar Questions
In a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠POC=(2212)∘
View SolutionIn a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠BDC=2∠POC
View SolutionIn a square ABCD, diagonals meet at O. P is a point on BC, such that OB= BP. Show that:
∠BOP=3∠COP
View SolutionABC is an equilateral triangle, P is a point in BC such that BP : PC =2 : 1.
Prove that : 9AP2=7AB2
View SolutionIn parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP=BQ. Show that:
(i) ΔAPD≅ΔCQB
(ii) AP=CQ
(iii) ΔAQB≅ΔCPD
(iv) AQ=CP
(v) APCQ is a parallelogram.

View SolutionA point O lies inside a ΔABC. Show that OA+OB+OC>12(AB+BC+CA).
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC.
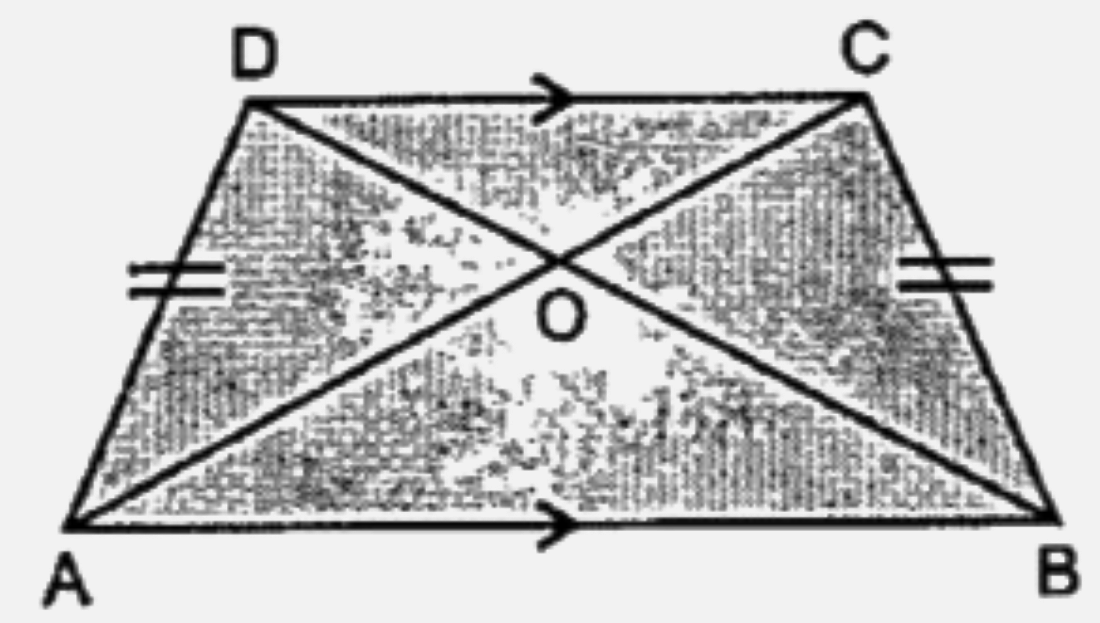
Prove that :
(i) ∠DAB=∠CBA
(ii) ∠ADC=∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2AD.
Prove that :
(i) BP bisects angle B.
(ii) Angle APB = 90∘
View SolutionThe point O is outside the ∠ABC. Show that 2(OA+OB+OC)>AB+BC+CA.
View SolutionThe given figure shows parallelogram ABCD. Points M and N lie in diagonal BD such that DM=BN
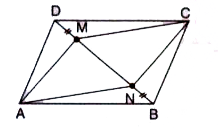 .
.
Prove that:
(i) ΔDMC≅ΔBNA and so CM=AN.
(ii) ΔAMD≅ΔCNB and so AM=CN.
(iii) ANCM is a parallelogram.
View Solution
