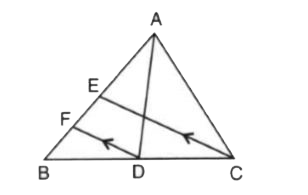
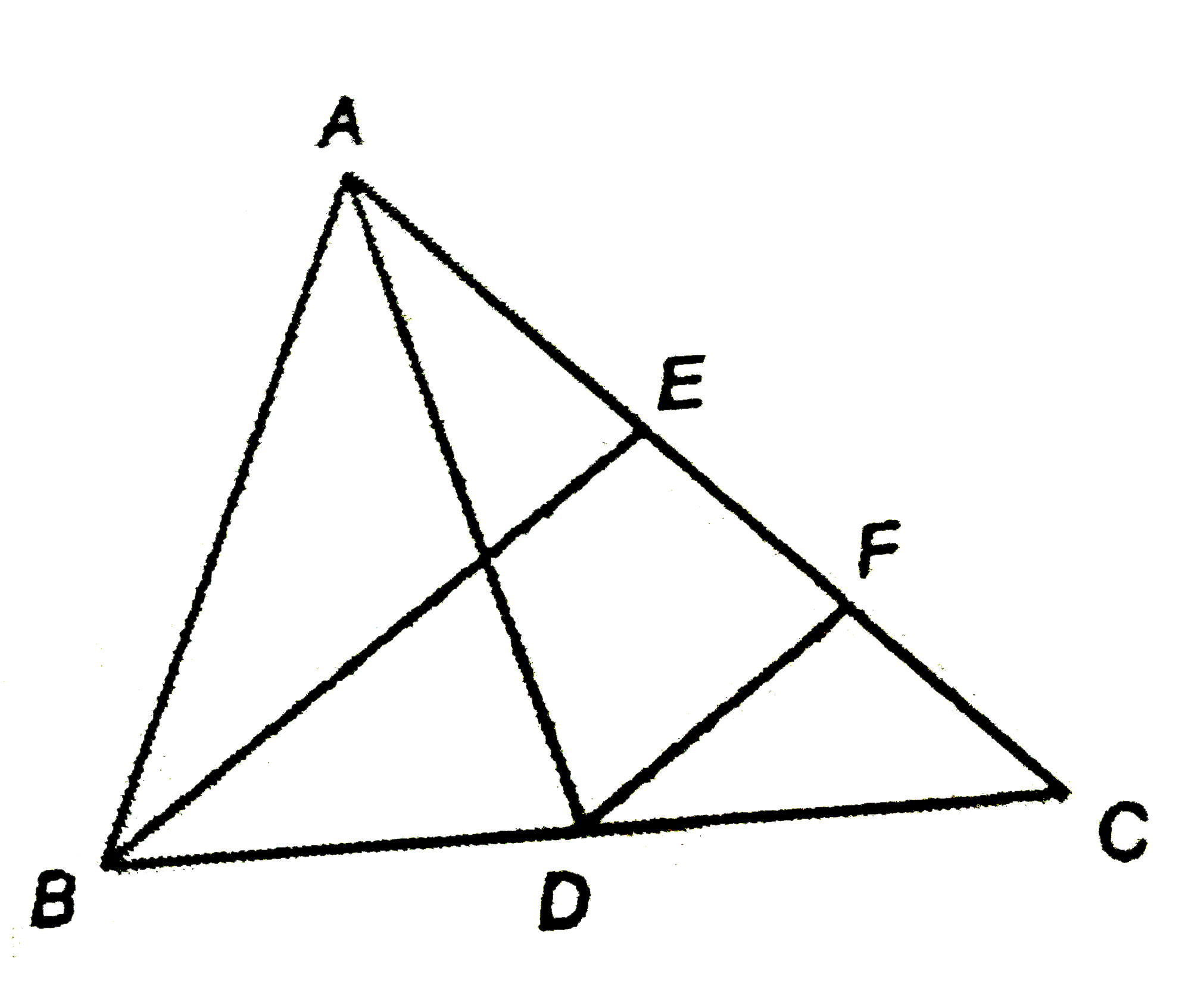
In the given figure, AD and CE are medians and DF∣∣CE. Prove that : FB=14AB.
The correct Answer is:FB=14AB
Step by step video & image solution for In the given figure, AD and CE are medians and DF||CE. Prove that : FB=(1)/(4)AB. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MID-POINT THEOREMBOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION
15 Videos
- MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)BOOK - ICSECHAPTER - MID-POINT AND ITS CONVERSE(INCLUDING INTERCEPT THEOREM)EXERCISE - EXERCISE 12(B)
23 Videos
- PYTHAGORAS THEORAMBOOK - ICSECHAPTER - PYTHAGORAS THEORAMEXERCISE - QUESTIONS
9 Videos
Similar Questions
In the given figure, AD and CE are medians and DF||CE. Prove that : Fb=14AB.
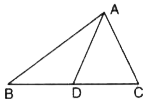
View SolutionIn the given figures, AB > AC and D is any point on BC.
Prove that : AB >AD.
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC
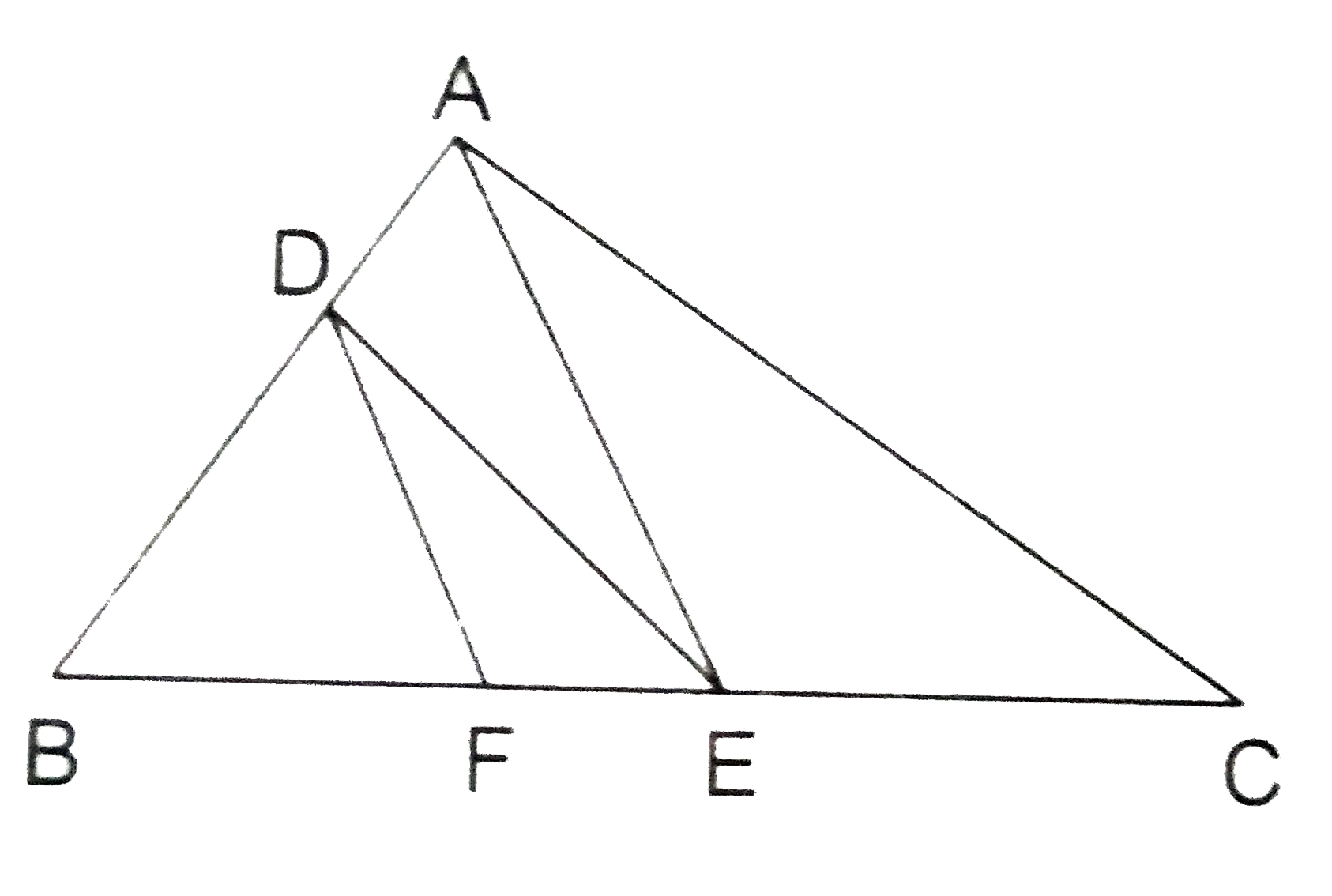
View SolutionIn the given figure, DE||ACandDF||AE.
Prove that BFFE=BEEC

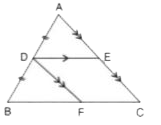
View SolutionIn the given figure D is mid-point of AB. DE//BC and DF //AC . Prove that : DE = BF
View SolutionIn the adjoining figure. AD and BE are two medians of ΔABC. IfDF||BE,then prove thatCF=14AC.
View SolutionIn the given figure, AC=AE,AB=AD and ∠BAD=∠EAC. Prove that BC=DE.
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

View SolutionIn the given figure AD and CE are two altitude of △ABC. Prove that. △AEF~△CDF
View SolutionIn the given figure , BC = CE and ∠1=∠2.
Prove that :
ΔGCB=ΔDCB .
View Solution
