In the given figure, ∠BAC=30∘ . Show that BC is equal to the radius of the circumcircle of ΔABC whose centre is O.

Join OB and OC.
∠BOC=2∠BAC=2×30∘=60∘
OB=OC⇒∠OBC=∠OCB=x∘ ( say )
∴in ∠OBC , we have
∠BOC+∠OBC+∠OCB=180∘⇒60∘+2x∘=180∘⇒x=60∘
Thus, each angle of ΔBOC is 60∘
∴ΔBOC is an equilateral triangle
∴OB=OC=BC
Hence, BC is the radius of the circumcircle.
Topper's Solved these Questions
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - EXERCISE 12C
26 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Multiple Choice Questions (Mcq)
5 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - Exercise 12A
22 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBOOK - RS AGGARWALCHAPTER - BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONEXERCISE - EXERCISE 17B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
Similar Questions
Knowledge Check
If R is the radius of the circumcircle of the ΔABCandΔ is its area then
AR=a+b+c2BR=a+b+cΔCR=abc4ΔDR=abcΔIn a triangle ABC if b=2,B=30∘ then the area of the circumcircle of triangle ABC in square units is :
AπB2πC4πD6πIn a right -angled triangle ABC, ∠ABC=90∘,AB=5cm and BC = 12 cm . The radius of t he circumcircle of the triangle ABC is
A7.5 cmB6 cmC6.5 cmD7cm
In a triangle ABC if b=2,B=30∘ then the area of the circumcircle of triangle ABC in square units is :
View SolutionIn triangle ABC,a:b:c=4:5:6. The ratio of the radius of the circumcircle to that of the incircle is____.
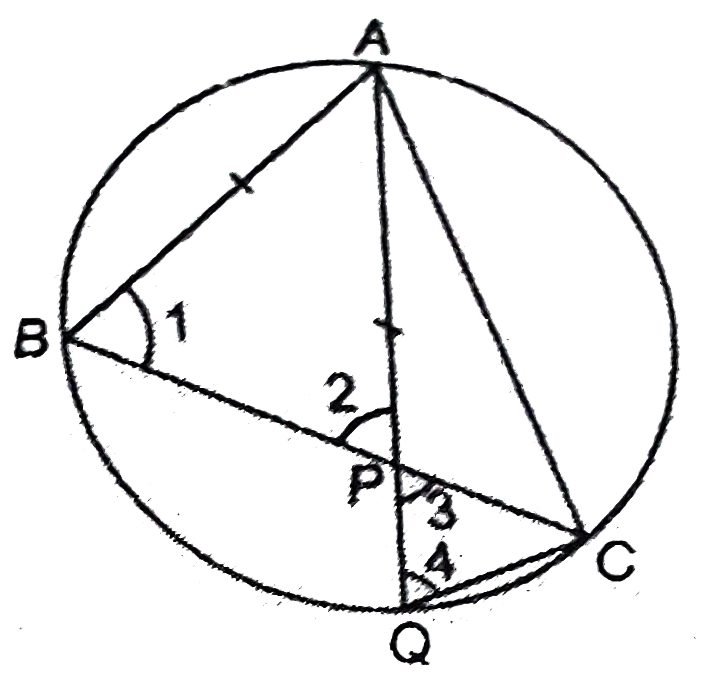
View SolutionIn given figure, ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
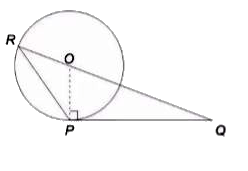
View SolutionIn the given figure, triangle ABC is drawn such that AB is tangent to a circle at A whose radius is 10 cm and BC passes through centre of the circle. Point C lies on the circle. If BC = 36 cm and AB 24cm,then what is the area (in cm2) of triangle ABC?
View SolutionIn the given figure, ΔPQR is drawn such that PQ is tangent to a circle whose radius is 10 cm and QR passes through centre of the circle. Point R lies on the circle. If QR=36cm, then what is the area (in cm2 ) of ΔPQR ?
View Solution

