In Figure., ABC
is a triangle in which ∠BAC=300.
Show that BC
is the radius of the circumcircle of ABC,
whose centre is O.

Step by step video & image solution for In Figure., A B C is a triangle in which /_B A C=30^0dot Show that B C is the radius of the circumcircle of A B C , whose centre is Odot by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.

View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn triangle ABC,a:b:c=4:5:6. The ratio of the radius of the circumcircle to that of the incircle is____.
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).

View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960

View SolutionBisector AD of ∠BAC of ABC passes through the centre O of the circumcircle of ABC as shown in figure. Prove that AB=AC.
View SolutionIn a triangle ABC (a+b)cosC+(a+c)cosB+(b+c)cosAsinA+sinB+sinC=100 then the area of the circumcircle of triangle ABC is
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
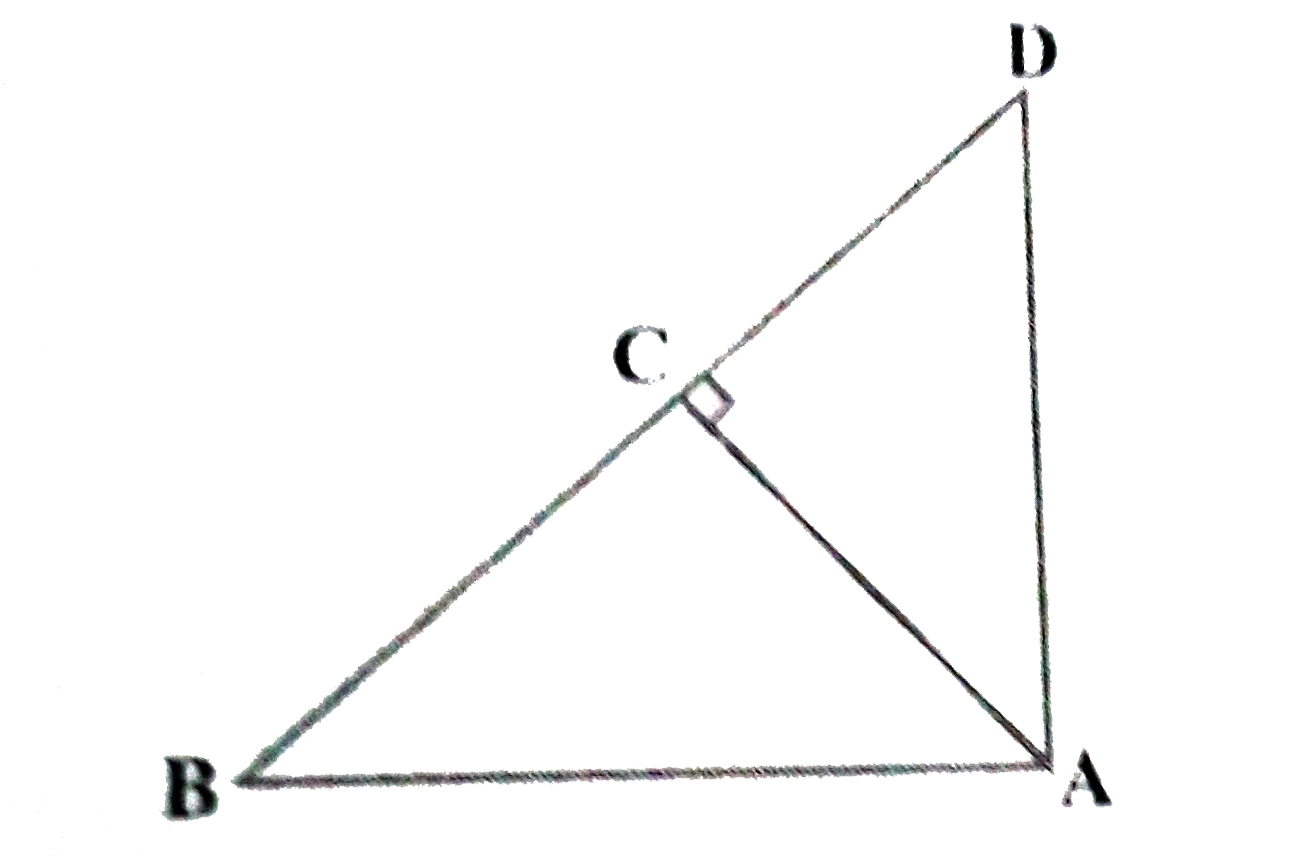
View SolutionIn triangle ABC,∠A=600,∠B=400,and∠C=800. If P is the center of the circumcircle of triangle ABC with radius unity, then the radius of the circumcircle of triangle BPC is 1 (b) √3 (c) 2 (d) √3 2
View Solution
