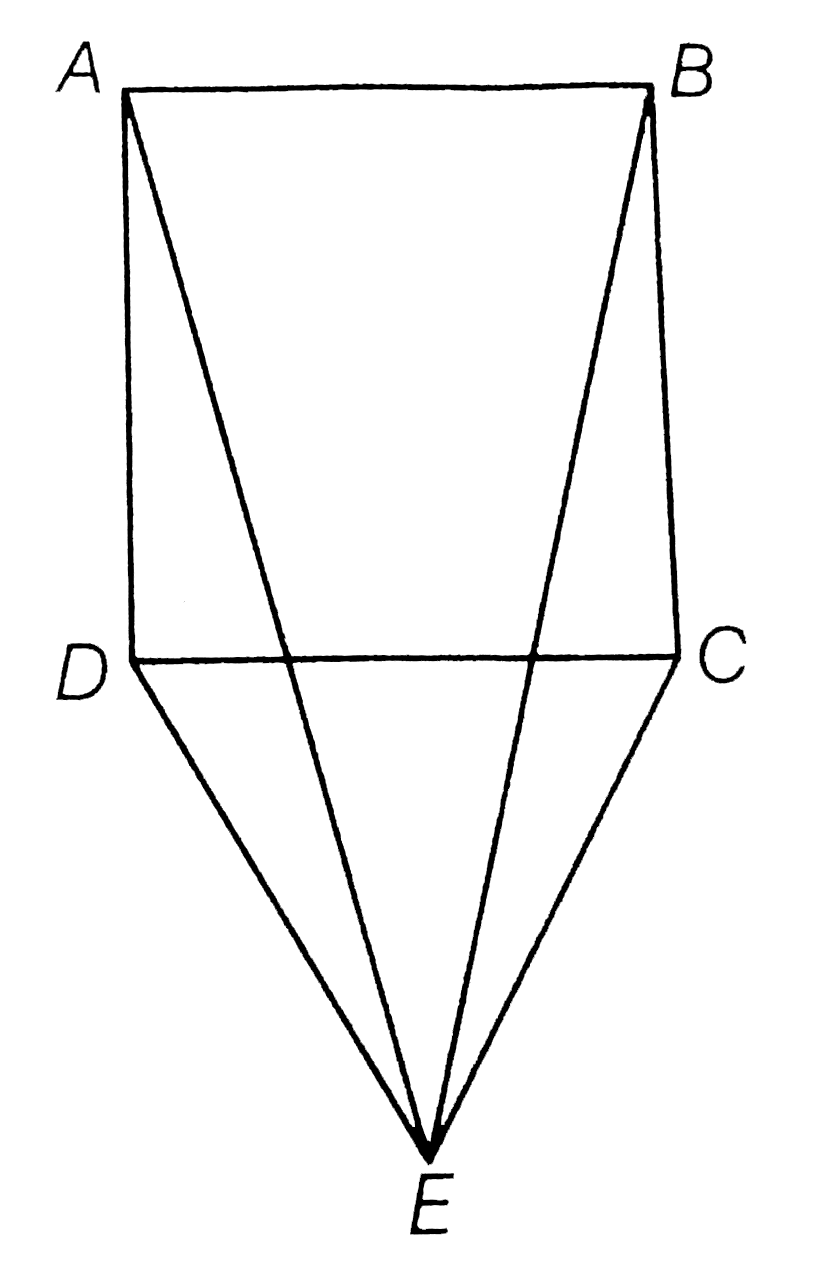
In the given figure, ΔCDE is an equilateral triangle on a side CD of a square ABCD. Show that ΔADE≅ΔBCE.
Video Solution
Text Solution
GIVEN A square ABCD and an equilateral ΔCDE on side CD.
TO PROVE ΔADE≅ΔBCE.
PROOF In ΔADEandΔBCE, we have
AD=BC (sides of the same square)
DE=CE (sides of an equilateral triangle)
∠ADE=∠BCE [each equal to (90∘+60∘)=150∘]
∴ ΔADE≅ΔBCE [by SAS-criteria].
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
ABCD is a square and ABE is an equilateral triangle outside the square then
A∠ACE=12∠ABEB∠ACE=∠ABEC∠ACE=2∠ABEDNone of theseIn the figure ΔABE is an equilateral triangle in a square ABCD. Find the value of angle x in degrees :
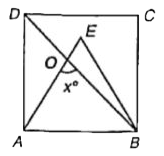 A60∘B45∘C75∘D90∘
A60∘B45∘C75∘D90∘The equilateral triangle ABP lies inside the square ABCD. Find ∠CPD.
A150°B145°C155°D160°
In the given figure, PQR is an equilateral triangle and QRST is a square. Then ∠PSR=
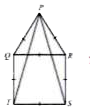
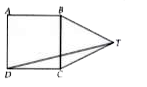
View SolutionIn the given figure, ABCD is a square and ΔBCT is an equilateral triangle. Find ∠BTD.
View SolutionIn the given figure equilateral triangle EDC surmounts the square ABCD. α=
View SolutionIn the given figure, ΔABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.
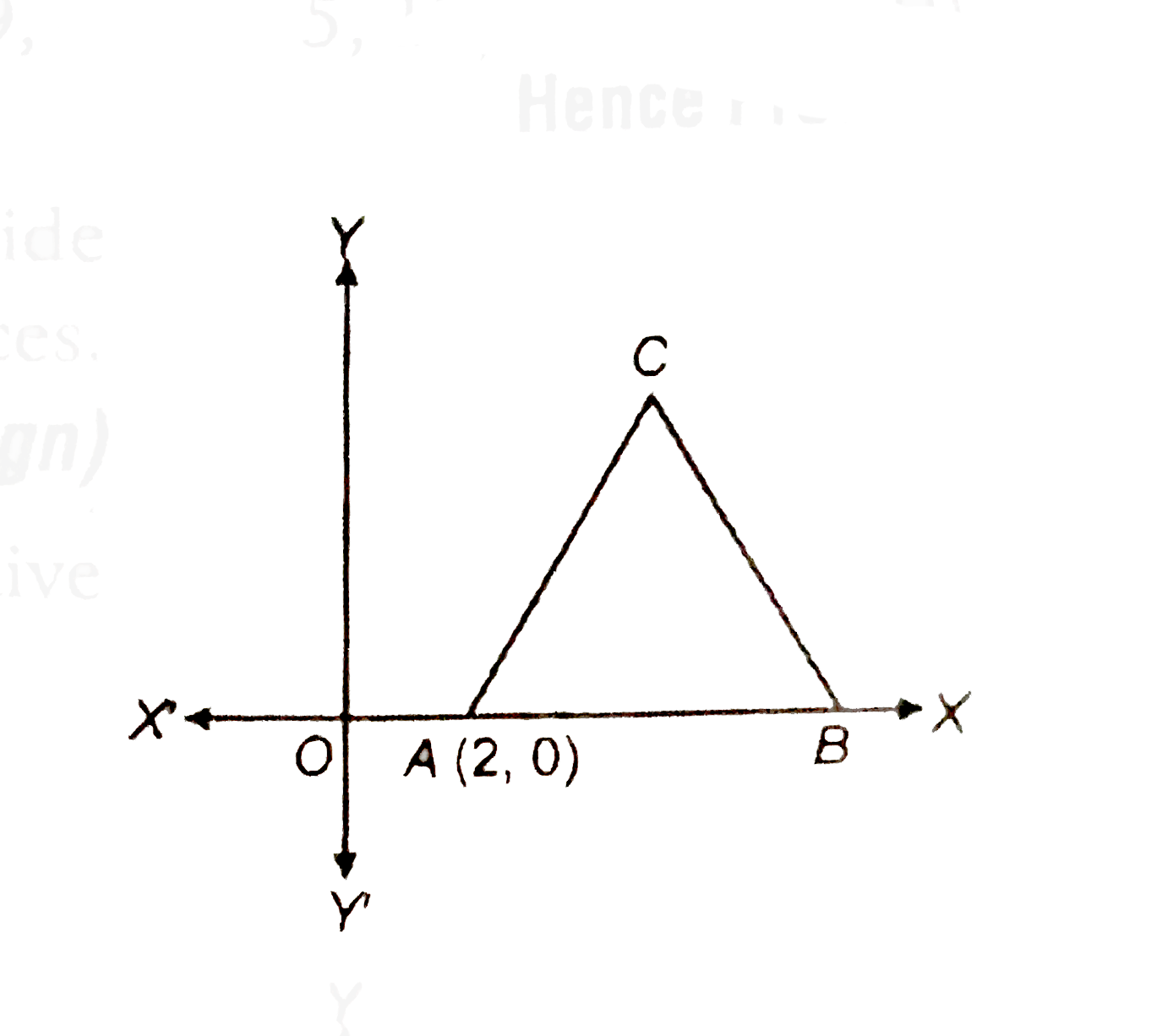
View SolutionThe given figure shows a square ABCD and an equilateral triangle ABP Calculate
View Solution