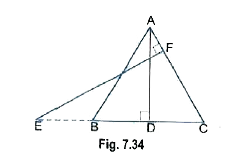
In the given figure, E is a point on side CB produced of an isosceles ΔABC with AB=AC.. If AD⊥BCandEF⊥AC, prove tha ΔABD~ΔECF
To prove that triangle ΔABD∼ΔECF, we will follow these steps:
Step 1: Identify the Given Information
We are given that ΔABC is an isosceles triangle with AB=AC, and AD⊥BC and EF⊥AC.
Step 2: Establish Corresponding Angles
Since AB=AC in triangle ABC, by the property of isosceles triangles, the angles opposite to the equal sides are equal. Thus, we have:
∠ABC=∠ACB
Step 3: Identify Right Angles
From the problem, we know:
- AD⊥BC implies ∠ADB=90∘
- EF⊥AC implies ∠EFC=90∘
Step 4: Compare Angles in Triangles
Now we will compare the angles in triangles ABD and ECF:
- In triangle ABD:
- ∠ADB=90∘
- ∠ABC=∠ACB (from Step 2)
- In triangle ECF:
- ∠EFC=90∘
- ∠ECF=∠ABC (since ∠ABC=∠ACB)
Step 5: Establish Angle-Angle (AA) Similarity
Now we can establish similarity using the AA criterion:
1. ∠ADB=∠EFC=90∘
2. ∠ABC=∠ECF
Since both triangles share two equal angles, we can conclude:
ΔABD∼ΔECF
Conclusion
Thus, we have proved that ΔABD is similar to ΔECF.
---
We are given that ΔABC is an isosceles triangle with AB=AC, and AD⊥BC and EF⊥AC.
Since AB=AC in triangle ABC, by the property of isosceles triangles, the angles opposite to the equal sides are equal. Thus, we have:
∠ABC=∠ACB
From the problem, we know:
- AD⊥BC implies ∠ADB=90∘
- EF⊥AC implies ∠EFC=90∘
Now we will compare the angles in triangles ABD and ECF:
- In triangle ABD:
- ∠ADB=90∘
- ∠ABC=∠ACB (from Step 2)
- ∠EFC=90∘
- ∠ECF=∠ABC (since ∠ABC=∠ACB)
Now we can establish similarity using the AA criterion:
1. ∠ADB=∠EFC=90∘
2. ∠ABC=∠ECF
ΔABD∼ΔECF
Thus, we have proved that ΔABD is similar to ΔECF.
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
In figure E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD⊥BCandEF⊥AC, prove thatΔABD~ΔECF.

View SolutionIn the given Fig. 7 .34, AB = AC. E is a point on CB produced. If AD is perpendicular to BC and EF perpendicular to AC, prove that ΔABD is similar to ΔCEF.
View Solution
Knowledge Check
In the given figure, △ABC is an isosceles triangle, in which AB=AC, AD⊥BC, BC = 6cm and AD = 4cm. The length of AB is:
दी गयी आकृति में, त्रिभुज ABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC,AD⊥BC, BC = 6सेमी तथा AD =4 सेमी है | AB की लंबाई कितनी है ? A4 cmB6 cmC7 cmD5 cm
A4 cmB6 cmC7 cmD5 cmIn a △ABC,AB = AC and AD⊥BC, then :
AAB<ADBAB>ADCAB=ADDAB≤AD
D is a point on side BC of ΔABC such that AD=AC. Show that AB>AD.
View SolutionIn the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
View SolutionIf D any point on the BC of an isosceles triangle ABC then prove that AB>AD and AC>AD.

View SolutionD is a point on side BC of ΔABCsuch that AD = AC(see Fig. 7.47).Show that AB > AD.
View SolutionABC is an isosceles triangle with AB = AC. Draw AP⊥BC to show that ∠B=∠C.
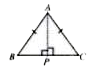
View SolutionΔABC is an isosceles, with AB=AC. If P be any point on the side BC. Prove that AP<AB.
View Solution
