In the given figure, if DE || BC, AE = 8 cm, EC = 2 cm and BC = 6 cm, then find DE
The correct Answer is:4.8 cm
To solve the problem, we will use the properties of similar triangles. Here’s a step-by-step solution:
Step 1: Identify the triangles
We have two triangles, triangle ADE and triangle ABC. Since DE is parallel to BC, we can use the properties of similar triangles.
Step 2: Establish similarity
Since DE || BC, we know that:
- Angle DAE = Angle BAC (common angle)
- Angle ADE = Angle ABC (corresponding angles)
Thus, by the Angle-Angle (AA) criterion for similarity, triangle ADE is similar to triangle ABC.
Step 3: Set up the proportion
For similar triangles, the ratios of corresponding sides are equal. Therefore, we can write the following proportion:
AEEC=DEBC
Step 4: Substitute known values
We know:
- AE = 8 cm
- EC = 2 cm
- BC = 6 cm
Substituting these values into the proportion gives us:
82=DE6
Step 5: Simplify the left side
Calculating the left side:
82=4
So, we have:
4=DE6
Step 6: Cross-multiply to solve for DE
Cross-multiplying gives us:
4×6=DE
DE=24
Step 7: Solve for DE
Now, we need to find DE in terms of the total length AE + EC:
AE+EC=8+2=10
Now we can set up the proportion again:
DEBC=DE6=810
Step 8: Solve for DE
Cross-multiplying gives us:
10⋅DE=48
DE=4810=4.8 cm
Final Answer
Thus, the length of DE is:
DE=4.8 cm
---
We have two triangles, triangle ADE and triangle ABC. Since DE is parallel to BC, we can use the properties of similar triangles.
Since DE || BC, we know that:
- Angle DAE = Angle BAC (common angle)
- Angle ADE = Angle ABC (corresponding angles)
For similar triangles, the ratios of corresponding sides are equal. Therefore, we can write the following proportion:
AEEC=DEBC
We know:
- AE = 8 cm
- EC = 2 cm
- BC = 6 cm
82=DE6
Calculating the left side:
82=4
So, we have:
4=DE6
Cross-multiplying gives us:
4×6=DE
DE=24
Now, we need to find DE in terms of the total length AE + EC:
AE+EC=8+2=10
Now we can set up the proportion again:
DEBC=DE6=810
Cross-multiplying gives us:
10⋅DE=48
DE=4810=4.8 cm
Thus, the length of DE is:
DE=4.8 cm
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
In the figure, EF || AC, BC = 10 cm, AB = 13 cm and EC = 2 cm, find AF
View SolutionIn the given figure, DE//BC,AE=15cm,EC=9cm,NC=6cmandBN=24cm.
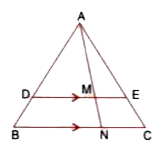
Find lengths of ME and DM.
View SolutionIn the given figure, DE//BC,AE=15cm,EC=9cm,NC=6cmandBN=24cm.
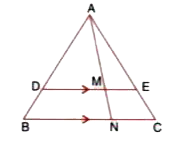
Write all possible pairs of similar triangles.
View SolutionIn the adjoining figure, AB=8cm,DM=6cmandBC=6cm. Find the length of DN

View SolutionIn the given figure if DE||BC, find the value of x.
View SolutionIn the given figure, DE // BC and AE : EC = 5 : 4. Find :
DE : BC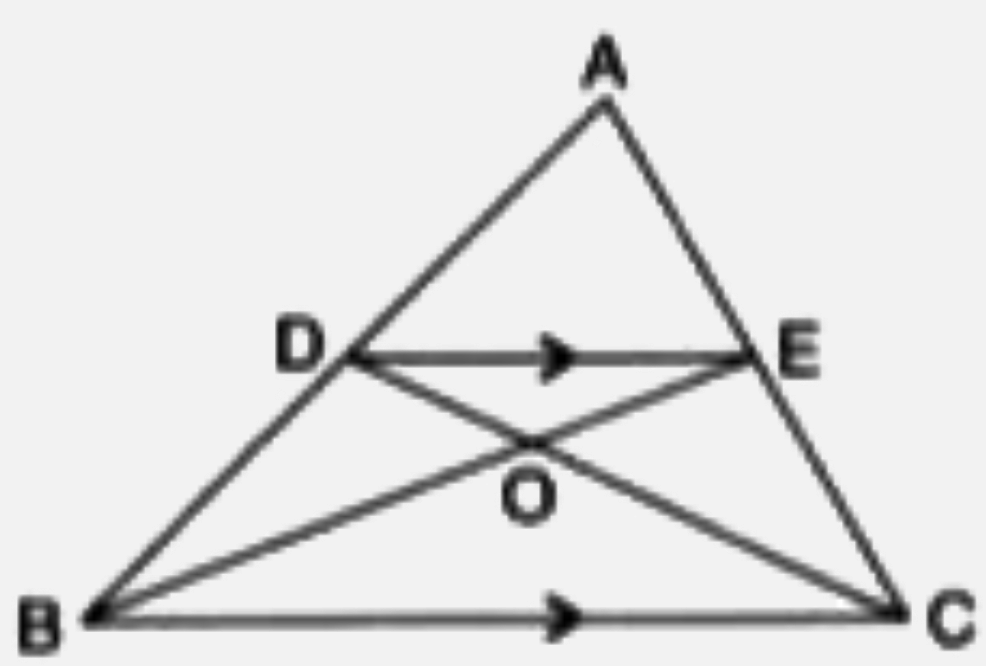
View SolutionIn the given figure, DE // BC and AE : EC = 5 : 4. Find :
DO : DC

View SolutionIn the given figure, AP = 8 cm, BP = 22 cm, AQ = 12 cm and QC = 8 cm

If PQ = 14 cm, find BC.
View Solutionin a figure DE||BC AD=3cm, BD =4cm and BC=14cm, then DE equals
View SolutionIn the given figure, ΔABC~ΔADE. If AE:EC=4:7andDE=6.6cm, find BC. If *x' be the length of the perpendicular from A to DE, find the length of perpendicular from A to BC in terms of ‘x'.

View Solution
