In the given figure, if TP and TQ are tangents to a circle with centre O, so that ∠POQ=110∘, then ∠PTQ is
110∘
90∘
80∘
70∘
The correct Answer is:D
To solve the problem, we need to find the measure of angle PTQ given that angle POQ is 110 degrees and TP and TQ are tangents to the circle with center O.
1. Identify the Given Information:
- We have a circle with center O.
- TP and TQ are tangents to the circle at points P and Q respectively.
- Angle POQ = 110 degrees.
2. Use the Property of Tangents:
- The radius of the circle at the point of tangency is perpendicular to the tangent. Therefore, we have:
- Angle OPT = 90 degrees (since OP is the radius and TP is the tangent).
- Angle OQT = 90 degrees (since OQ is the radius and TQ is the tangent).
3. Consider the Quadrilateral OPTQ:
- The sum of the interior angles of a quadrilateral is 360 degrees. Thus, we can write:
Angle OPT+Angle POQ+Angle OQT+Angle PTQ=360∘
4. Substitute Known Values:
- We know:
- Angle OPT = 90 degrees
- Angle POQ = 110 degrees
- Angle OQT = 90 degrees
- Substituting these values into the equation gives:
90+110+90+Angle PTQ=360
5. Simplify the Equation:
- Adding the known angles:
290+Angle PTQ=360
6. Solve for Angle PTQ:
- To find Angle PTQ, we subtract 290 from both sides:
Angle PTQ=360−290
Angle PTQ=70∘
Final Answer:
Thus, the measure of angle PTQ is 70 degrees.
- We have a circle with center O.
- TP and TQ are tangents to the circle at points P and Q respectively.
- Angle POQ = 110 degrees.
- The radius of the circle at the point of tangency is perpendicular to the tangent. Therefore, we have:
- Angle OPT = 90 degrees (since OP is the radius and TP is the tangent).
- Angle OQT = 90 degrees (since OQ is the radius and TQ is the tangent).
- The sum of the interior angles of a quadrilateral is 360 degrees. Thus, we can write:
Angle OPT+Angle POQ+Angle OQT+Angle PTQ=360∘
- We know:
- Angle OPT = 90 degrees
- Angle POQ = 110 degrees
- Angle OQT = 90 degrees
- Substituting these values into the equation gives:
90+110+90+Angle PTQ=360
- Adding the known angles:
290+Angle PTQ=360
- To find Angle PTQ, we subtract 290 from both sides:
Angle PTQ=360−290
Angle PTQ=70∘
Thus, the measure of angle PTQ is 70 degrees.
Topper's Solved these Questions
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION-A (ANSWER THE FOLLOWING)
3 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - SECTION-A (ANSWER THE FOLLOWING) 16 (a)
1 Videos
- SAMPLE PAPER 2019BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - SAMPLE PAPER 2019EXERCISE - 38B
1 Videos
- CBSE BOARDS 2020BOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - CBSE BOARDS 2020EXERCISE - QUESTION
41 Videos
- X BoardsBOOK - X BOARD PREVIOUS YEAR PAPER ENGLISHCHAPTER - X BoardsEXERCISE - All Questions
481 Videos
Similar Questions
If TP and TQ are the two tangents to a circle with centre O so that ∠POQ=110∘, then ∠PTQ is equal to
View SolutionIn the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.

View SolutionIn Figure 2, AB and AC are tangents to the circle with centre O such that angle BAC = 40°. Then angle BOC is equal to
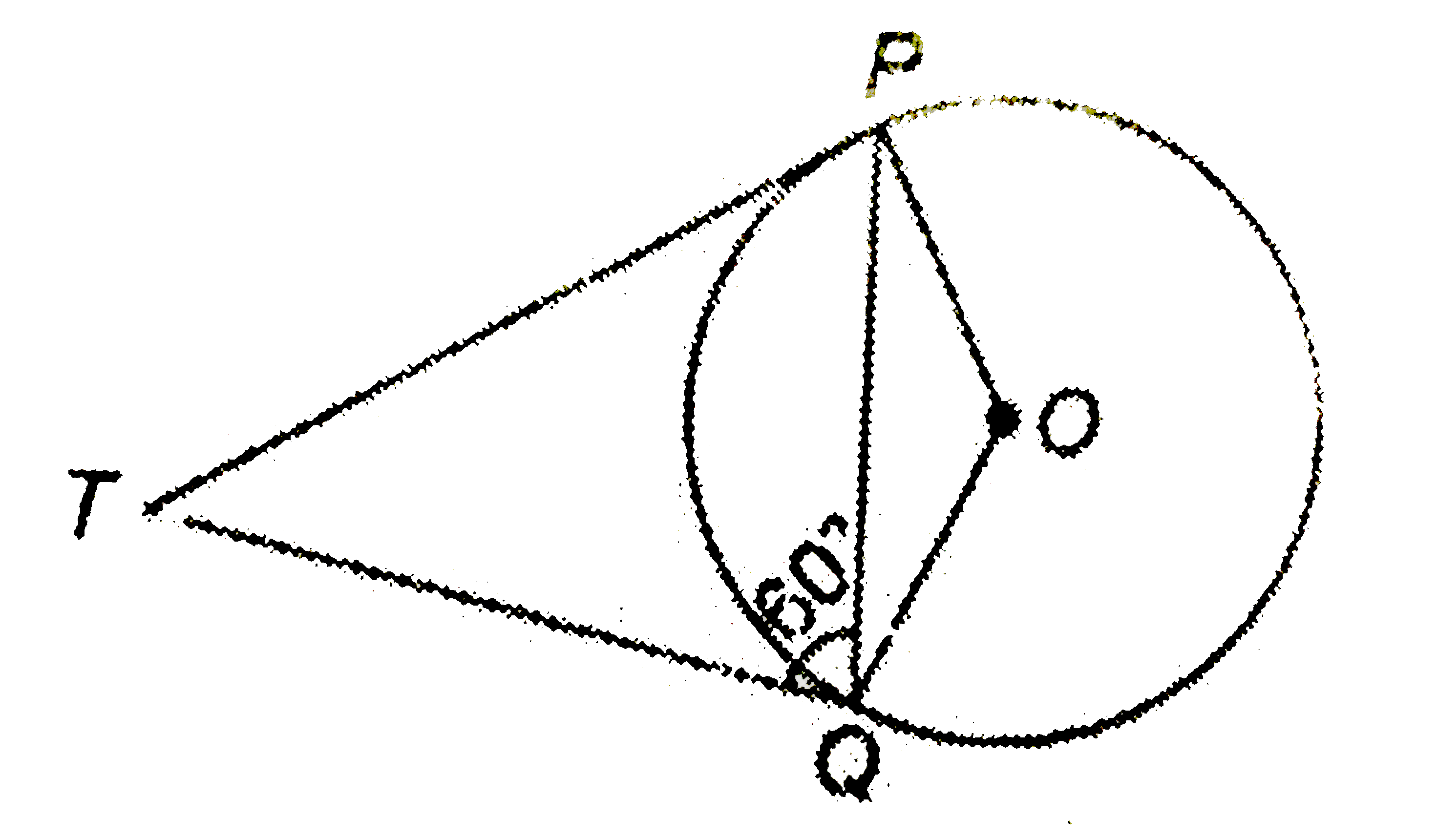
View SolutionIn the given figure, TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP=60∘. Find angelOPQ.
View SolutionIn figure PQ is tangent to the circle with centre at O at the point B , if ∠AOB=100∘, then ∠ABP is equal to

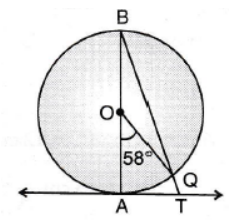
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
View SolutionIn Figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘ . Write the measure of ∠OAB .
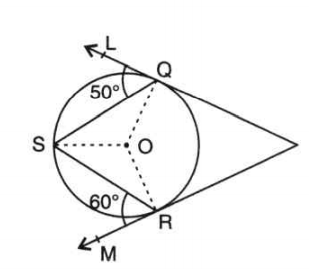
View SolutionIn the given figure, PQL and PRM are two tangents to the circle with centre O at the point Q and R respectively. If S is a point on the circle such that angle SQL = 50° and sk... o angle SRM = 60°. Find the reflex angle QOR.
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘
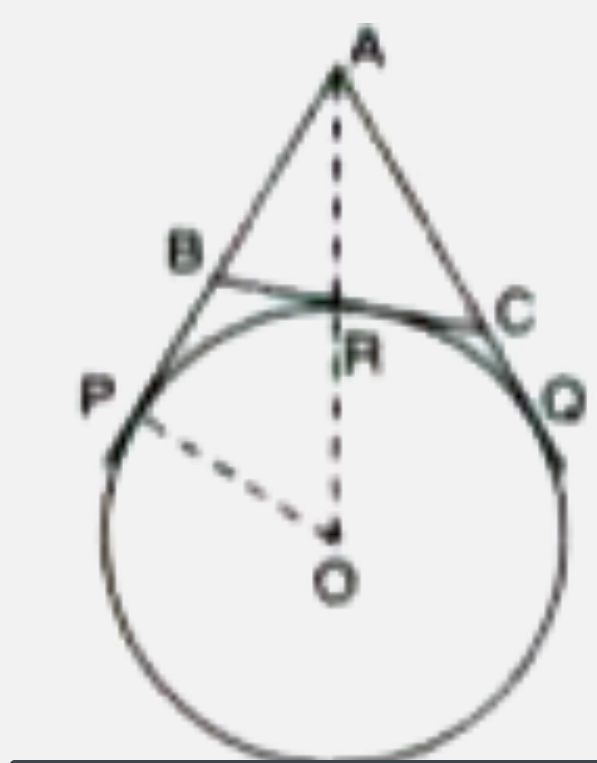
View SolutionIn the given figure AP and AQ are tangents to the circle with centre O. BC is tangent at point R on it.
If OA=17 cm and radius of the circle =8cm, find the perimeter of the triangle ABC.
View Solution
