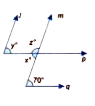
In the given figure, l || m and p || q. Find the value of x,y,z,t.
To solve the problem, we need to find the values of angles x, y, z, and t given that lines l and m are parallel, and lines p and q are also parallel.
1. Identify the Angles:
- We have two pairs of parallel lines: l∥m and p∥q.
- The lines intersect at some point, creating angles x, y, z, and t.
2. Use the Property of Vertically Opposite Angles:
- When two lines intersect, the angles opposite each other are equal. Therefore, if we denote the angle opposite to z as z′, we can say:
z=z′
- If z is given as 80∘, then:
z=80∘
3. Find the Corresponding Angles:
- Since l∥m and q is a transversal, the angles z and t are corresponding angles. Thus:
t=z=80∘
4. Find the Remaining Angles:
- Now, since p∥q and l is a transversal, angles y and x are also corresponding angles. Therefore:
y=z=80∘
x=t=80∘
5. Summarize the Values:
- We have found the values of all angles:
x=80∘,y=80∘,z=80∘,t=80∘
Final Answer:
- The values of x, y, z, and t are all 80∘.
- We have two pairs of parallel lines: l∥m and p∥q.
- The lines intersect at some point, creating angles x, y, z, and t.
- When two lines intersect, the angles opposite each other are equal. Therefore, if we denote the angle opposite to z as z′, we can say:
z=z′
- If z is given as 80∘, then:
z=80∘
- Since l∥m and q is a transversal, the angles z and t are corresponding angles. Thus:
t=z=80∘
- Now, since p∥q and l is a transversal, angles y and x are also corresponding angles. Therefore:
y=z=80∘
x=t=80∘
- We have found the values of all angles:
x=80∘,y=80∘,z=80∘,t=80∘
- The values of x, y, z, and t are all 80∘.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
In the given figure, find the value of z
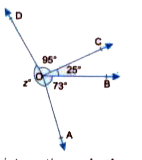 A167∘B157∘C147∘D137∘
A167∘B157∘C147∘D137∘
In the given figure, l||mandp||q. Find the angles x, y and z
 View Solution
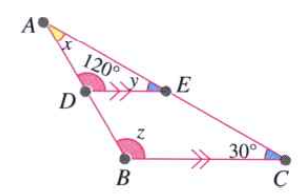
View SolutionIn the given figure, find x,y and z.
 View Solution
View SolutionIn the given figure, AB||CDandBC||AD. Find the values of x, y and z
 View Solution
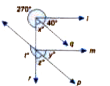
View SolutionIn the given figure, l||mandp||q. Find the angles x, y, z and t.
 View Solution
View SolutionIn the given figure, l||m||nandp||q||r. Find the angles x,y, z and t.
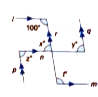 View Solution
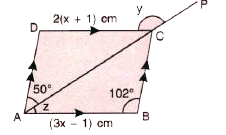
View SolutionIn the given figure, ABCD is a parallelogram. Find the values of x, y and z
 View Solution
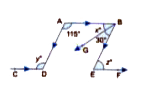
View SolutionIn the given figure, AB||CD||EFandAD∣∣BE. Find x,y and z
 View Solution
View Solution