In the given figure, AB||CD and a transversal PQ cuts them at L and M respectively. If ∠QMD=1000, find all other angles.
To solve the problem step by step, we will use the properties of angles formed by parallel lines and a transversal.
1. Identify Given Information:
- We have two parallel lines: AB and CD.
- A transversal PQ intersects these lines at points L and M.
- We are given that ∠QMD=100°.
2. Determine Vertically Opposite Angles:
- Since ∠QMD (angle 2) is given as 100°, the angle directly opposite to it, ∠MLQ (angle 1), is also 100° because vertically opposite angles are equal.
- Therefore, ∠MLQ=100°.
Hint: Remember that vertically opposite angles are always equal.
3. Find Angle 3:
- ∠QMD (angle 2) and ∠3 (the angle adjacent to ∠QMD on line CD) form a linear pair. The sum of angles in a linear pair is 180°.
- Thus, we can write:
\(
∠QMD + ∠3 = 180°
\)
\(
100° + ∠3 = 180°
\)
\(
∠3 = 180° - 100° = 80°
\)
Hint: Linear pairs of angles add up to 180°.
4. Determine Angle 1 Again:
- Since ∠3 (angle 3) is 80°, and ∠MLQ (angle 1) is vertically opposite to ∠3, we have:
\(
∠MLQ = ∠3 = 80°
\)
Hint: Use the property of vertically opposite angles again.
5. Find Corresponding Angles:
- Now we can find the remaining angles using the property of corresponding angles:
- ∠4 (angle 4) is corresponding to ∠QMD (angle 2), so:
\(
∠4 = ∠QMD = 100°
\)
- ∠5 (angle 5) is corresponding to ∠MLQ (angle 1), so:
\(
∠5 = ∠MLQ = 80°
\)
- ∠6 (angle 6) is corresponding to ∠QMD (angle 2), so:
\(
∠6 = ∠QMD = 100°
\)
- ∠7 (angle 7) is corresponding to ∠3, so:
\(
∠7 = ∠3 = 80°
\)
Hint: Corresponding angles are equal when two lines are parallel and cut by a transversal.
6. Summarize All Angles:
- Now we have found all angles:
- ∠1=80°
- ∠2=100°
- ∠3=80°
- ∠4=100°
- ∠5=80°
- ∠6=100°
- ∠7=80°
Final Answer:
- The angles are:
- ∠1=80°
- ∠2=100°
- ∠3=80°
- ∠4=100°
- ∠5=80°
- ∠6=100°
- ∠7=80°
- We have two parallel lines: AB and CD.
- A transversal PQ intersects these lines at points L and M.
- We are given that ∠QMD=100°.
- Since ∠QMD (angle 2) is given as 100°, the angle directly opposite to it, ∠MLQ (angle 1), is also 100° because vertically opposite angles are equal.
- Therefore, ∠MLQ=100°.
- ∠QMD (angle 2) and ∠3 (the angle adjacent to ∠QMD on line CD) form a linear pair. The sum of angles in a linear pair is 180°.
- Thus, we can write:
\(
∠QMD + ∠3 = 180°
\)
\(
100° + ∠3 = 180°
\)
\(
∠3 = 180° - 100° = 80°
\)
- Since ∠3 (angle 3) is 80°, and ∠MLQ (angle 1) is vertically opposite to ∠3, we have:
\(
∠MLQ = ∠3 = 80°
\)
- Now we can find the remaining angles using the property of corresponding angles:
- ∠4 (angle 4) is corresponding to ∠QMD (angle 2), so:
\(
∠4 = ∠QMD = 100°
\)
- ∠5 (angle 5) is corresponding to ∠MLQ (angle 1), so:
\(
∠5 = ∠MLQ = 80°
\)
- ∠6 (angle 6) is corresponding to ∠QMD (angle 2), so:
\(
∠6 = ∠QMD = 100°
\)
- ∠7 (angle 7) is corresponding to ∠3, so:
\(
∠7 = ∠3 = 80°
\)
- Now we have found all angles:
- ∠1=80°
- ∠2=100°
- ∠3=80°
- ∠4=100°
- ∠5=80°
- ∠6=100°
- ∠7=80°
- The angles are:
- ∠1=80°
- ∠2=100°
- ∠3=80°
- ∠4=100°
- ∠5=80°
- ∠6=100°
- ∠7=80°
Topper's Solved these Questions
Similar Questions
In the given figure, line l || m and a transversal n cuts them at P and Q respectively. If ∠1=750, find all other angles.
View SolutionIn the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively, If ∠CMQ=600 find all other angles in the figure.
View SolutionIn the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn the given figure l||mandp||q. Find the angle x,y, z
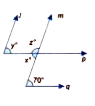
View SolutionIn the given figure, l||mandp||q. Find the angles x, y and z

View SolutionIn Figure, AB and CD are parallel lines and transversal EF intersects them at P and Q respectively. If ∠APR=250, ∠RQC=300and ∠CQF=650, then
(a) x=550, y=400
(b) x=500, y=450
(c) x=600, y=350
(d) x=350, y=600
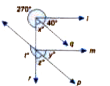
View SolutionIn the given figure, l||mandp||q. Find the angles x, y, z and t.
View SolutionIn the adjoining figure, transversal n cuts parallel lines l and m. If ∠5=65∘, find all other angles

View SolutionIn the given figure, a transversal n cuts two lines l and m if ∠1=700 and ∠7=800, is l ∣∣ m?
View SolutionIn the given figure, l||m||nandp||q||r. Find the angles x,y, z and t.
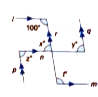
View Solution
