In the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQand∠PAC. If ∠BAQ=30∘, prove that :
(i) BD is a diameter of the circle.
(ii) ABC is an isosceles triangle

Step by step video & image solution for In the given figure PQ is a tangent to the circle at A. AB and AD are bisectors of angleCAQandanglePAC. If angleBAQ=30^(@), prove that : (i) BD is a diameter of the circle. (ii) ABC is an isosceles triangle by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the given PQ is a tangent to the circle at A. AB and AD are bisectors of ∠CAQ and ∠PAC. If ∠BAQ=30∘, prove that: BD is diameter of the circle.
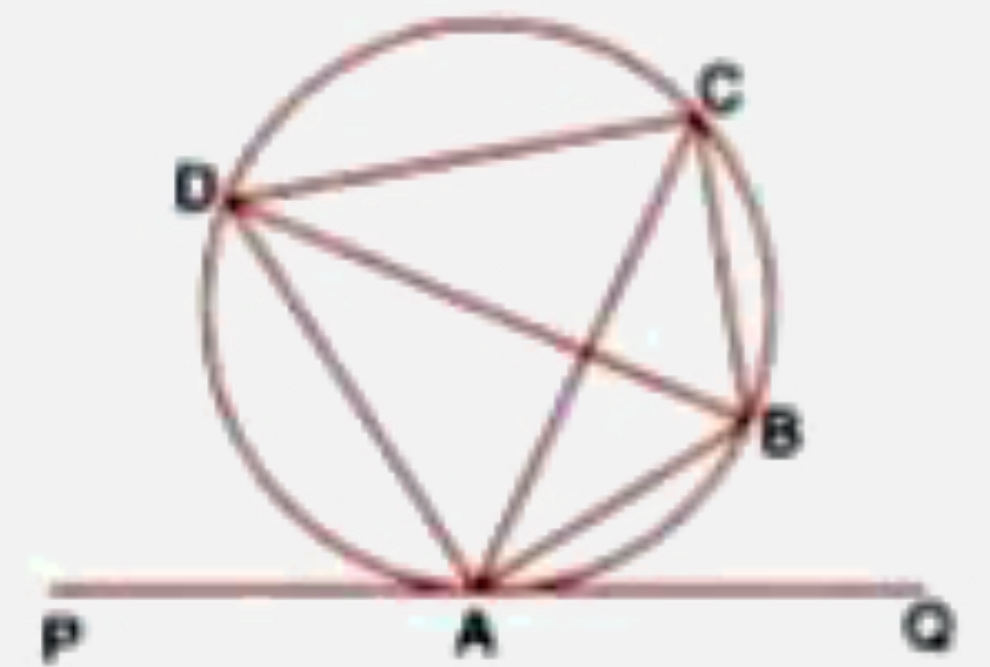
View SolutionIn the figure, O is the center of the circle and BO is the bisector of ∠ABC show that AB=BC
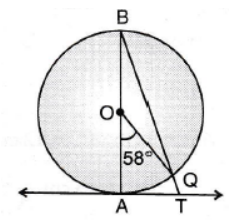
View SolutionIn the given figure, AB is diameter of a circle with centre O and AT is a tangent at ∠AOQ=58∘, find ∠ATQ.
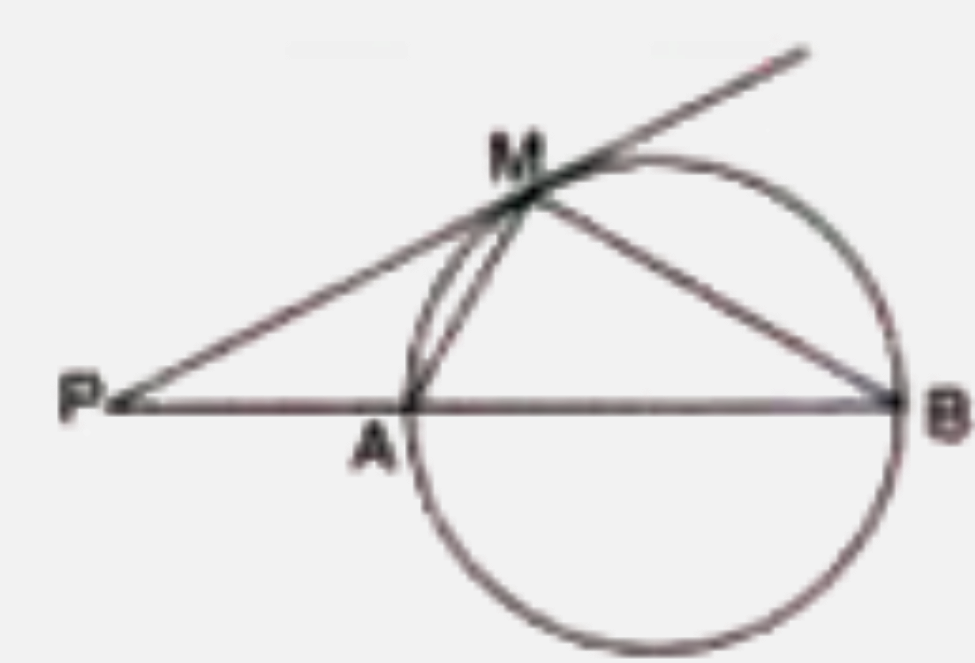
View SolutionIn the given figure PM is a tangent to the circle and PA =AM.
Prove that
(i) ΔPMB is isosceles
(ii) PAXxPB=MB2
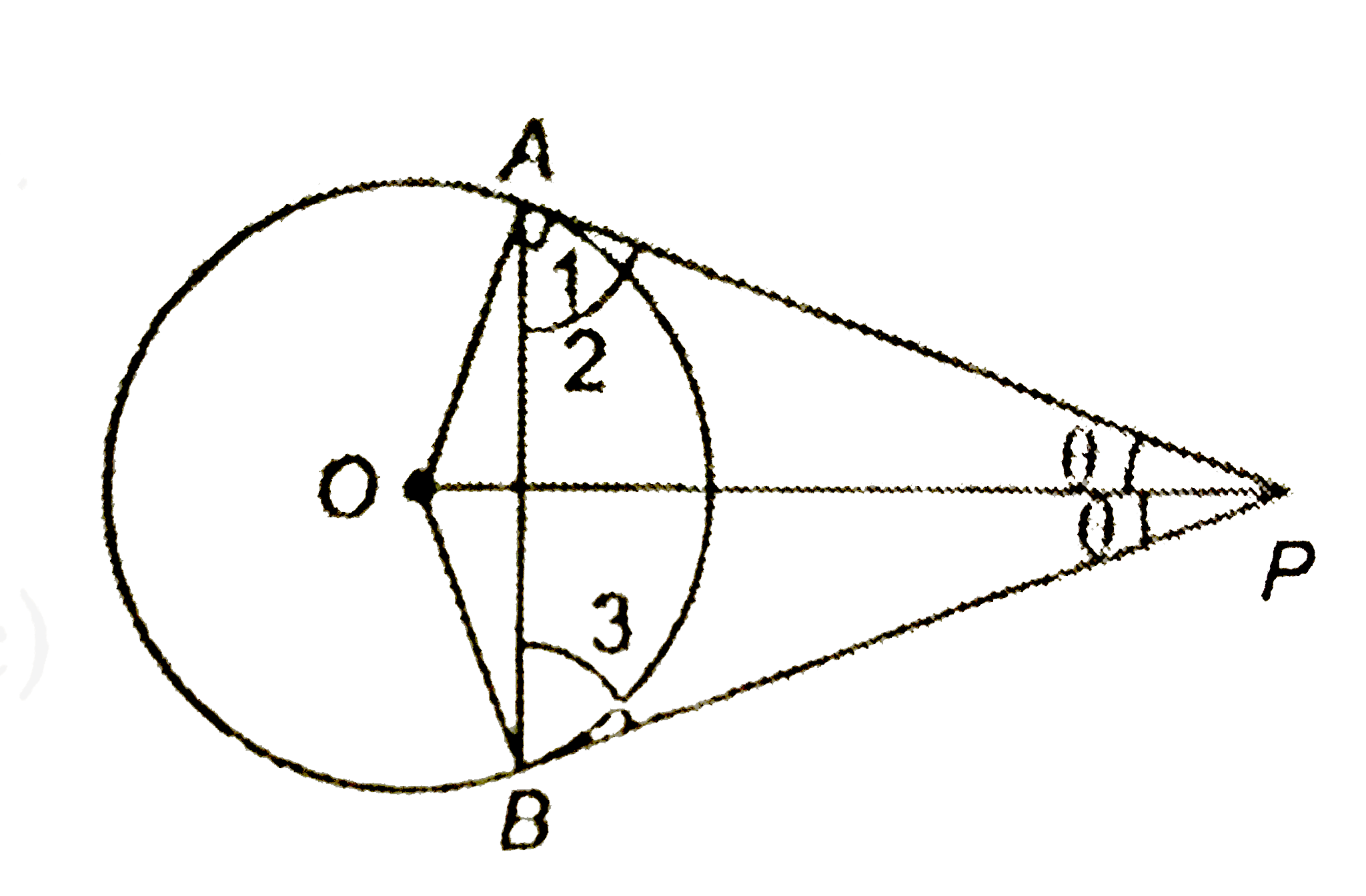
View SolutionIn the given figure, OP is equal to the diameter of the circle. Prove that △ABP is an equilateral triangle.
View SolutionIn the given figure, ∠DBC=58∘, BD is diameter of the circle. Calculate :
(i) ∠BDC (ii) ∠BEC (iii) ∠BAC

View SolutionIn the given figure, DE // BC.

Prove that ΔADEandΔABC are similar
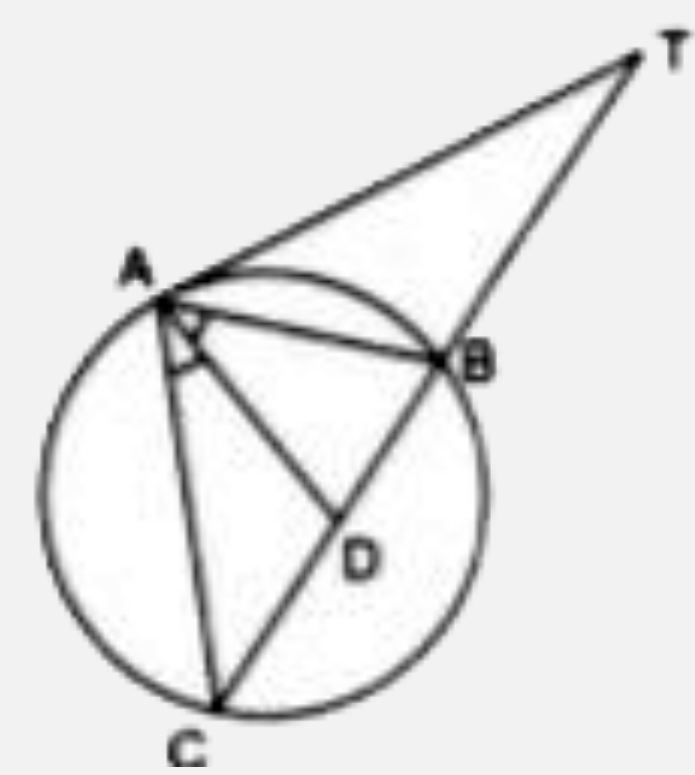
View SolutionIn the given TA is a tangent to the cirlce and TBC is a secant. If AD bisects angle BAC, prove that:ΔADT is isosceles.
View SolutionIf PQ is a tangent to the circle at R calculate
(i) ∠PRS
(i) ∠ROT
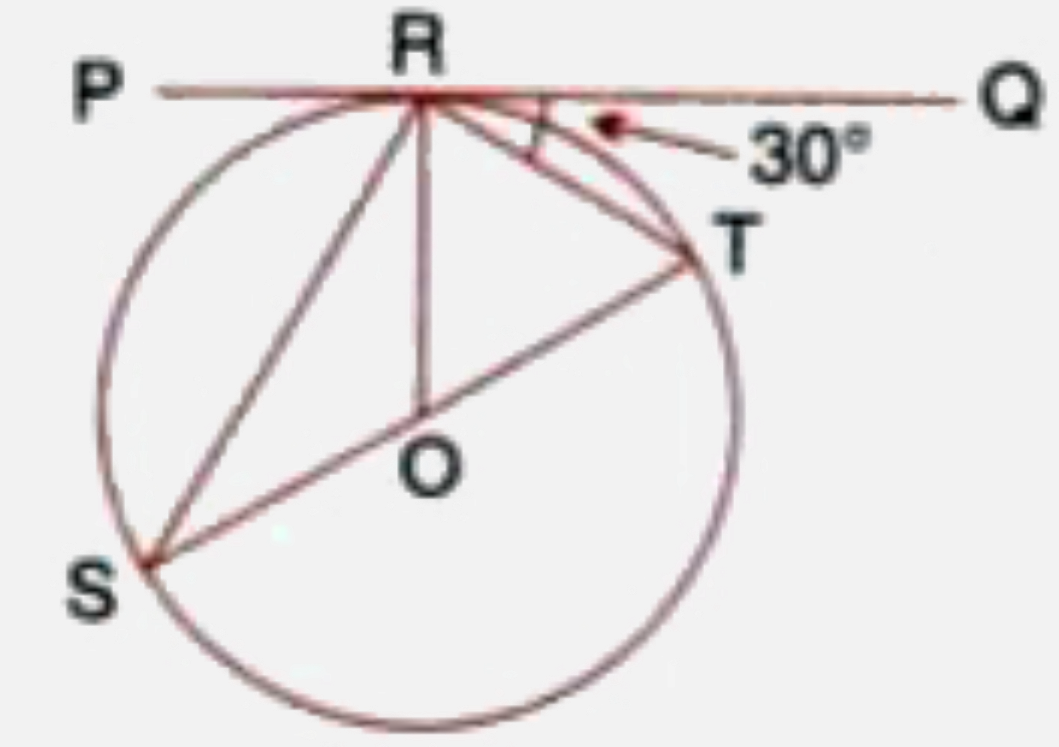
Given O is the centre of the circle and angle TRQ=30∘
View SolutionIn the following figure PQ is the tangent to the circle at A, DB is the diameter and O is the centre of the circle. If ∠ADB=30∘ and ∠CBD=60∘. Calculate :

(i) ∠QAB
(ii) ∠PAD
(iii) ∠CDB
View Solution
