Let ABCD be a rectangle and P be any point in its plane. Show that AP2+PC2=PB2+PD2.
The correct Answer is:NA
Let A≡(0,0),B≡(a,0),C≡(a,b)andD≡(0,b)
Let point P be (h,k).
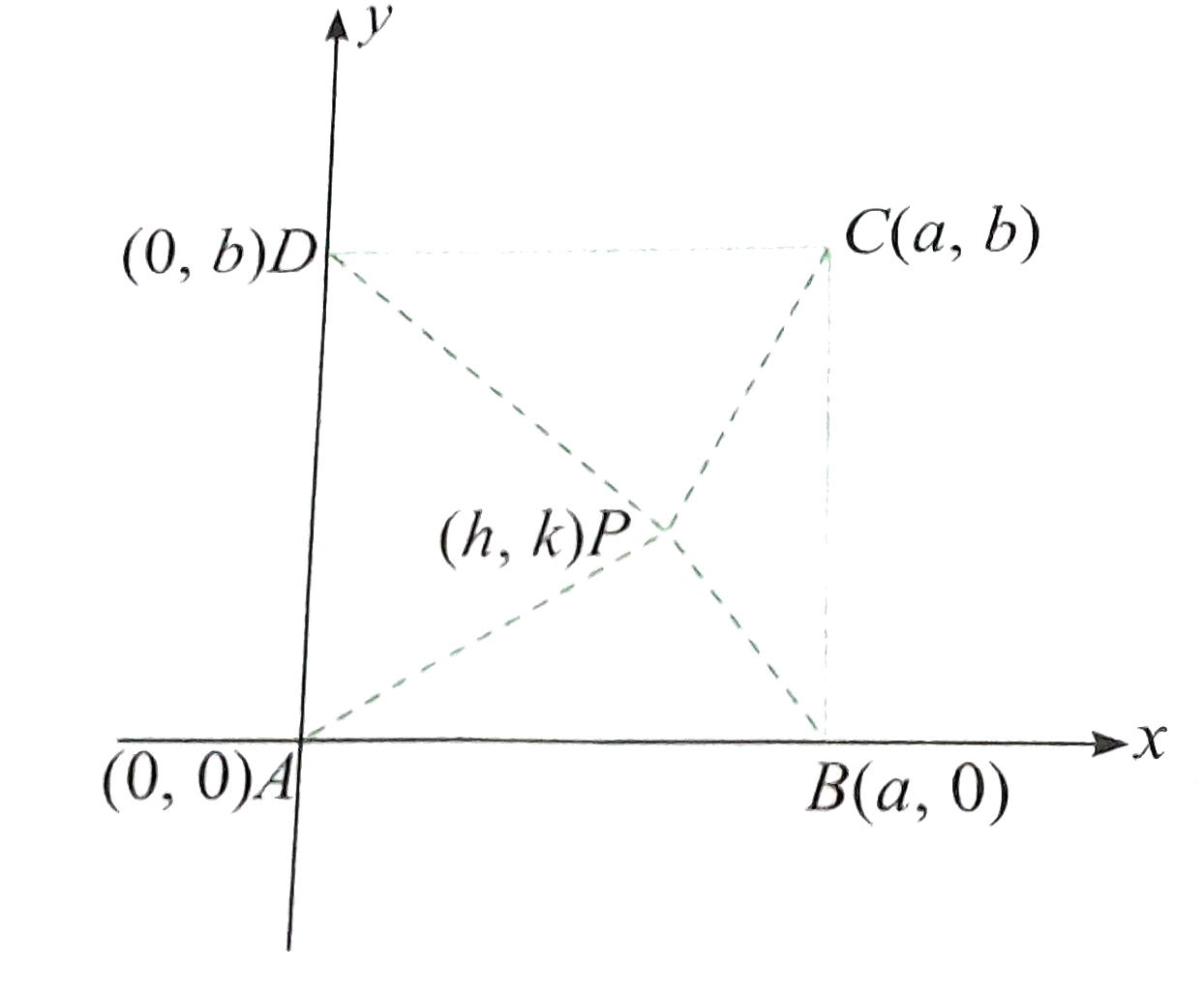
∴PA2+PC2=(h−0)2+(k−0)2+(h−a)2+(k−b)2=2h2+2k2−2k2−2ah−2bk+a2+b2
Also, PB2+PD2=(h−a)2+(k−0)2+(h−0)2+(k−b)2=2h2+2k2−2ah−2bk+a2+b2
Thus, PA2+PC2=PB2+PD2
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.3
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.4
8 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Let ABCD be a rectangle and P be any point in its plane. Show that AP2+PC2=PB2+PD2.
View SolutionIn Figure, ABCD and PQRC are rectangles and Q is the mid-point of AC . Prove that DP=PC (ii) PR=12 AC
View SolutionThe coordinates of A,B,C are (6,3),(−3,5),(4,−2) , respectively, and P is any point (x,y) . Show that the ratio of the area of PBC to that of ABC is |x+y−2|7.
View SolutionIn ABC,D is the mid-point of AB,P is any point of BC.CQPD meets AB in Q . Show that ar(BPQ)=12ar(ABC). TO PROVE : ar(BPQ)=12ar(ABC) CONSTRUCTION : Join CD.
View SolutionLet a,b,c,d and p be any non zero distinct real numbers such that (a2+b2+c2)p2−2(ab+bc+cd)p+(b2+c2+d2)=0. Then :
View SolutionIf the angles A,B,C of △ABC are in A.P., and its sides a, b, c are in Gp., show that a2,b2,c2 are in A.P.
View SolutionABCD is a parallelogram. P is a point on AD such that AP=13 AD and Q is a point on BC such that: CQ=13BC. Prove that AQCP is a parallelogram.
View SolutionABCD is a parallelogram. P is any point on CD. If ar (DPA)=15 cm2 and ar (APC)=20cm2, then ar (APB)=
(a) 15cm2 (b) 20cm2 (c) 35 cm2 (d) 30cm2
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View Solution
