ABCD
is a parallelogram. P
is any
point on CD.
If ar (DPA)=15 cm2
and ar (APC)=20cm2,
then ar (APB)=
(a) 15cm2
(b) 20cm2
(c)
35 cm2
(d)
30cm2
In ∣∣gm ABCD, P is any point on CD
AP, AC and PB are joined.
area(△DPA)=15cm2_____1
area(△APC)=20cm2__2
Now, Adding equation 1+2
ar(△ADC)=15+20=35cm2
∴ AC divides it into two triangle equal in area
area(△ACB)=area(△ADC)=35cm2
△APB and △ACB are on the same base and between the same parallels
area(△APB)=area(△ACB)=35cm2
Hence, option (c) is correct.
Topper's Solved these Questions
Similar Questions
Medians of ABC intersect at G . If ar (ABC)=27 cm2, then ar (ABGC)= 6 cm2 (b) 9 cm2 (c) 12 cm2 (d) 18cm2
View SolutionABCDEF . If BC=3cm , EF=4cm and ar(ABC)=54cm2 , then ar(DEF)= 108cm2 (b) 96cm2 (c) 48cm2 (d) 100cm2
View SolutionABCD is a rectangle with O as any point in its interior. If ar (AOD)=3 cm2and ar (BOC)=6 cm2, then area of rectangle ABCD is: 9cm2 (b) 12 cm2 (c) 15cm2 (d) 18 cm2,
View SolutionIn Figure, ABCDandFECG are parallelograms equal in area. If ar(AQE)=12cm2, then ar(IIgm)FGBQ)=
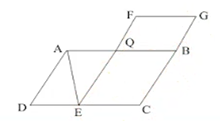
(a)12cm2
(b) 20cm2
(c) 24cm2
(d) 36cm2
View SolutionIn a ABC if D and E are mid-points of BC and AD respectively such that ar (AEC)=4 cm2 , then ar (BEC)= 4 cm2 (b) 6 cm2 (c) 8 cm2 (d) 12cm2
View SolutionA, B, C, D are mid-points of sides of a parallelogram PQRS. If ar (PQRS)=36cm2, then ar(ABCD)= 24 cm2 (b) 18 cm2 (c) 30 cm2 (d) 36 cm2
View SolutionThe area of a circle is 220 cm2 . The area of a square inscribed in it is (a) 49 cm2 (b) 70 cm2 (c) 140 cm2 (d) 150 cm2
View SolutionABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that: ar (ADO)=AR (CDO) ar ( ABP)= ar ( CBP)
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View SolutionIn a ABC, D, E, F are the mi-points of sides BC, CA and AB respectively. If ar(ABC)=16cm2, then ar (trapezium FBCE)= 4 cm2 (b) 8 cm2 (c) 12cm2 (d) 10cm2
View Solution