Let ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. la equals :
sinAsin(B+A2)
sinBsinCsin2(B+C2)
sinBsinCsin2(B+A2)
sinB+sinCsin2(B+A2)
The correct Answer is:C
To solve the problem, we need to find the value of la=maMa, where ma is the length of the internal angle bisector of angle A and Ma is the length of the internal angle bisector extended until it meets the circumcircle of triangle ABC.
1. Understanding the Angle Bisector Lengths:
The length of the internal angle bisector ma can be calculated using the formula:
ma=2bcb+ccos(A2)
where A is the angle at vertex A, and b and c are the lengths of the sides opposite to angles B and C respectively.
2. Finding the Extended Angle Bisector Length:
The length of the angle bisector extended to meet the circumcircle Ma can be expressed as:
Ma=2R⋅sinAsin(A2)
where R is the circumradius of triangle ABC.
3. Substituting into the Ratio:
Now we substitute ma and Ma into the expression for la:
la=maMa=2bcb+ccos(A2)2R⋅sinAsin(A2)
4. Simplifying the Expression:
We can simplify this expression:
la=bc⋅cos(A2)⋅sin(A2)R⋅sinA⋅(b+c)
Using the identity sinA=2sin(A2)cos(A2), we can further simplify:
la=bc⋅cos(A2)⋅sin(A2)R⋅2sin(A2)cos(A2)⋅(b+c)
Cancelling cos(A2) and sin(A2):
la=bc2R(b+c)
5. Final Expression:
Thus, the final expression for la is:
la=bc2R(b+c)
The length of the internal angle bisector ma can be calculated using the formula:
ma=2bcb+ccos(A2)
where A is the angle at vertex A, and b and c are the lengths of the sides opposite to angles B and C respectively.
The length of the angle bisector extended to meet the circumcircle Ma can be expressed as:
Ma=2R⋅sinAsin(A2)
where R is the circumradius of triangle ABC.
Now we substitute ma and Ma into the expression for la:
la=maMa=2bcb+ccos(A2)2R⋅sinAsin(A2)
We can simplify this expression:
la=bc⋅cos(A2)⋅sin(A2)R⋅sinA⋅(b+c)
Using the identity sinA=2sin(A2)cos(A2), we can further simplify:
la=bc⋅cos(A2)⋅sin(A2)R⋅2sin(A2)cos(A2)⋅(b+c)
Cancelling cos(A2) and sin(A2):
la=bc2R(b+c)
Thus, the final expression for la is:
la=bc2R(b+c)
Topper's Solved these Questions
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-4 : Matching Type Problems
2 Videos
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-5 : Subjective Type Problems
11 Videos
- SOLUTION OF TRIANGLESBOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SOLUTION OF TRIANGLESEXERCISE - Exercise-2 : One or More than One Answer is/are Correct
15 Videos
- SEQUENCE AND SERIES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - SEQUENCE AND SERIES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)
21 Videos
- STRAIGHT LINES BOOK - VIKAS GUPTA (BLACK BOOK) ENGLISHCHAPTER - STRAIGHT LINES EXERCISE - Exercise-5 : Subjective Type Problems
10 Videos
Similar Questions
Let ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The maximum value of the product (lalblc)×cos2(B−C2)×cos2(C−A)2)×cos2(A−B2) is equal to :
View SolutionLet ABC be a triangle inscribed in a circle and let la=maMa,lb=mbMb,lc=mcMc where ma,mb,mc are the lengths of the angle bisectors of angles A, B and C respectively , internal to the triangle and Ma,MbandMc are the lengths of these internal angle bisectors extended until they meet the circumcircle.
Q. The minimum value of the expression lasin2A+lbsin2B+lcsin2C is :
View SolutionABCD is a parallelogram. L and M are points on AB and DC respectively and AL=CM. prove that LM and BD bisect each other.
View SolutionLet ABC be a triangle with ∠B=900 . Let AD be the bisector of ∠A with D on BC. Suppose AC=6cm and the area of the triangle ADC is 10cm2. Find the length of BD.
View SolutionLet ABC be a triangle with ∠B=900 . Let AD be the bisector of ∠A with D on BC. Suppose AC=6cm and the area of the triangle ADC is 10cm2. Find the length of BD.
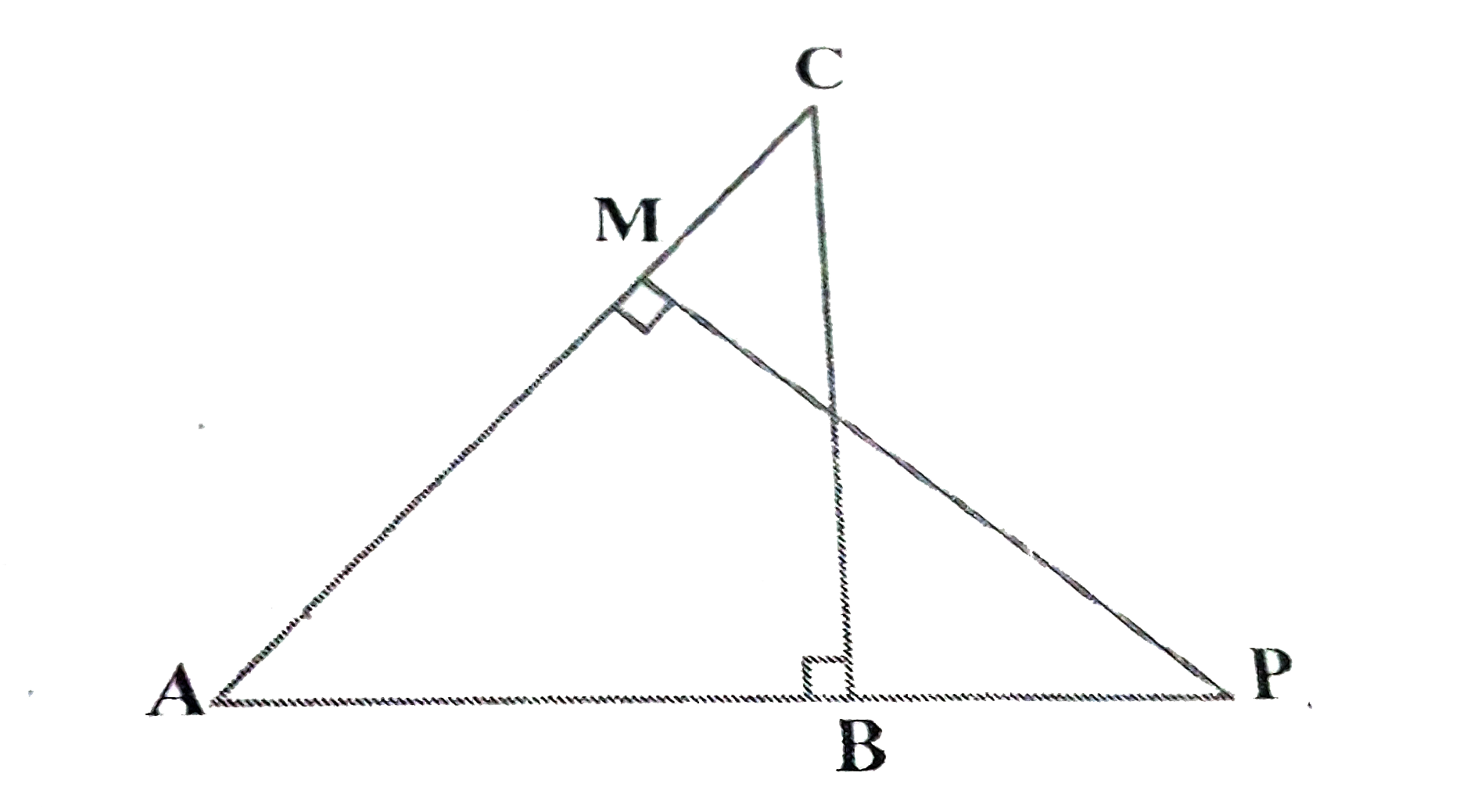
View SolutionIn figure ABC and AMP are two right triangles, right angles at B and M respectively. Prove that(i) ΔABC~ΔAMP (ii) CAPA=BCMP
View SolutionIn a right angled triangle ABC, right angled at B, BC=12cm and AB=5cm. The radius of the circle inscribed in the triangle (in cm) is :
View SolutionIn a ABC, If L and M are points on AB and AC respectively such that LM∣∣BC. Prove that: ar ( LBC)= ar ( MBC)
View SolutionIf ABC and AMP are two right triangles, right angled at B and M respectively such that ∠MAP=∠BAC . Prove that CAPA=BCMP
View SolutionMasses MAandMB hanging from the ends of strings of lengths LAandLB are executing simple harmonic motions. If their frequencies are fA=2fB, then
View Solution
