Let C0 be circle of radius 1. For n≥1, let Cn be a circle whose area equals the area of a squre inscibed in Cn−1. Then ∑∞i−0 Area (Ci) equals
π2
π−2π2
1π2
π2π−2
The correct Answer is:D
∞∑i− Area (Ci)=πr20+πr21+π22+πr23+....∞
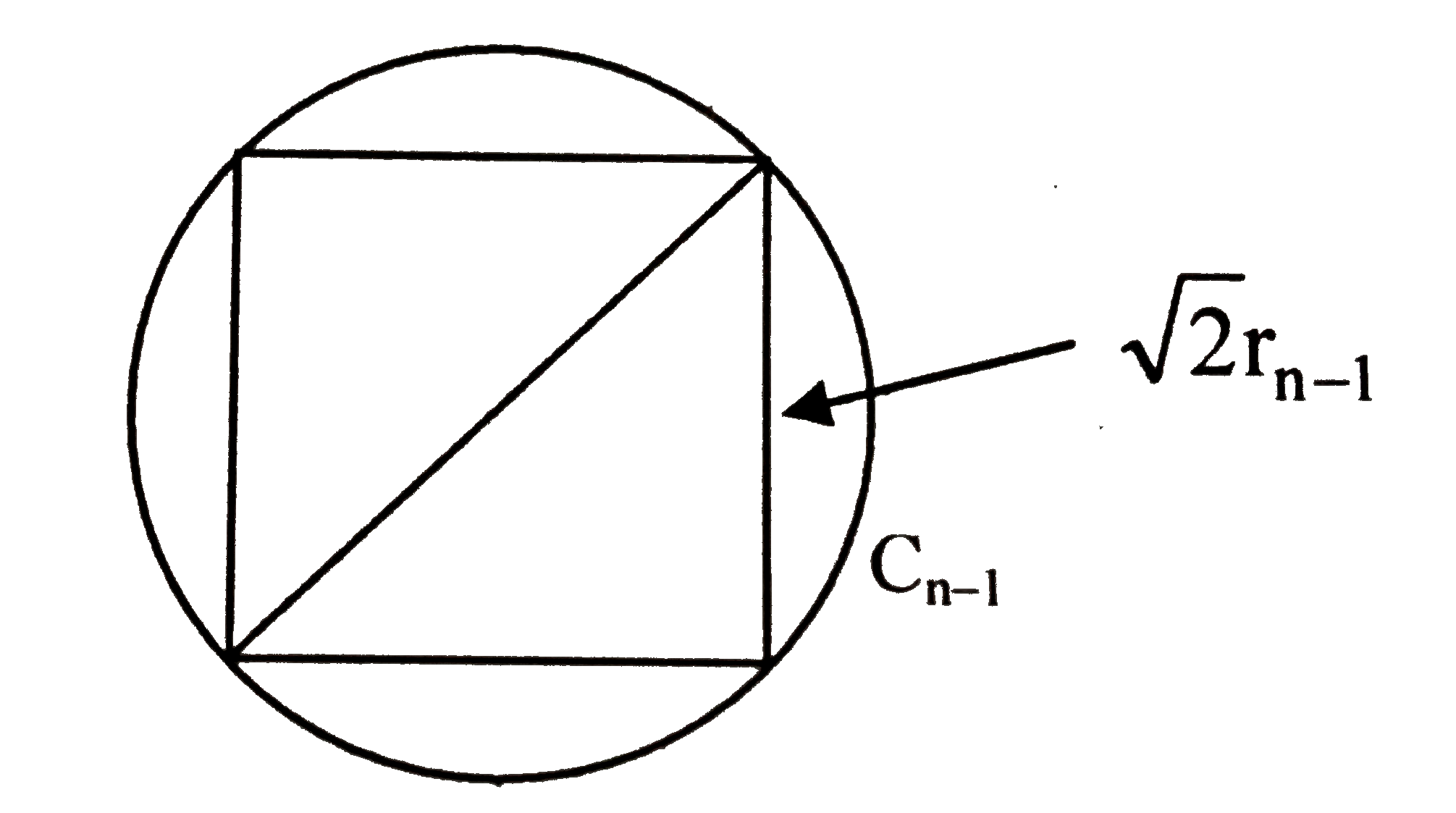
Area of Cn=πr2n=(√2r2n−1)2
r2n=2πr2n−1
so r21=2πr20,r22=2πr21
=2π(2πr20)
r23=2π(r22)=2π(2π2πr20)
So,∞∑i=o Area (Ci)=π[r20+2πr20+2π⋅2πr20+....∞]
=πr201−2π=π2r20π−2∀r0=1
=π2π−2
Topper's Solved these Questions
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-II MATHEMATICS
10 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - Part A - Mathematics
20 Videos
- KVPYBOOK - KVPY PREVIOUS YEARCHAPTER - KVPYEXERCISE - PART-2(MATHEMATICS)
10 Videos
- KVPY 2021BOOK - KVPY PREVIOUS YEARCHAPTER - KVPY 2021EXERCISE - PART II MATHEMATICS
4 Videos
Similar Questions
Let C0 be a circle of radius 1. For n≥1 let Cn be a circle whose area equals the are of a square inscribed in Cn−1 Then ∞∑i=0AreaCi equals (A) π2 (B) π−2π2 (C) 1π2 (D) π2π−2
View SolutionLet C1 be the circle of radius r>0 with centre at (0,0) and let C2 be the circle of radius r with centre at (r,0) .The length of the arc of the circle C1 that lies inside the circle C2 ,is
View Solution
Knowledge Check
If the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
AR1+R2=RBR21+R22=R2CR1+R2<RDR21+R22<R2If the area of a circle is A, radius of the circle is r and circumference of it is C, then
AAr=CBrC=2ACCA=r2DAC=r24If the area of a circle is A, radius of the circle is r and circumference of it is C, then
AAr=CBrC=rACCA=r2DAC=r24
What is the radius of a circle whose area is equal to the sum of the area of two circles whose radii are 20 cm and 21 cm .
View SolutionLet Cn be a circle of radius (23)n centered at the origin for n=0,1,2,.......andAn be the area of the region that is inside the circle C2n and outside the circle C2n+1 for n=0,1,2,.......The value of the ∞∑n=0An equals
View SolutionIf the area of circle is A1 and area of regular pentagon inscibed in the circle is A2, then find the ratio of area of two.
View SolutionIf radius of circle C1 is 2 times the radius of circle C2, then ratio of area C1 to that of C2 is
View SolutionIf the sum of the areas of two circles with radii R1 and R2 is equal to the area of a circle of radius R, then
View Solution
