Let f:R→Randg:R→R be respectively given by f(x)=|x|+1andg(x)=x2+1. Define h:R→R by h(x)={max{f(x),g(x)},ifx≤0andmin{f(x),g(x)},ifx>0.The number of points at which h(x) is not differentiable is Solution in Tamil
1
2
3
4
First we draw the graph, of y=|x|+1andy=x2+1
y=|x|+1={x+1,x≥0−x+1,x<0
y=x2+1 is a parabola having vertex at (0, 1) and concave upwards
Thus, the graphs of both functions are as shown in the following figure.
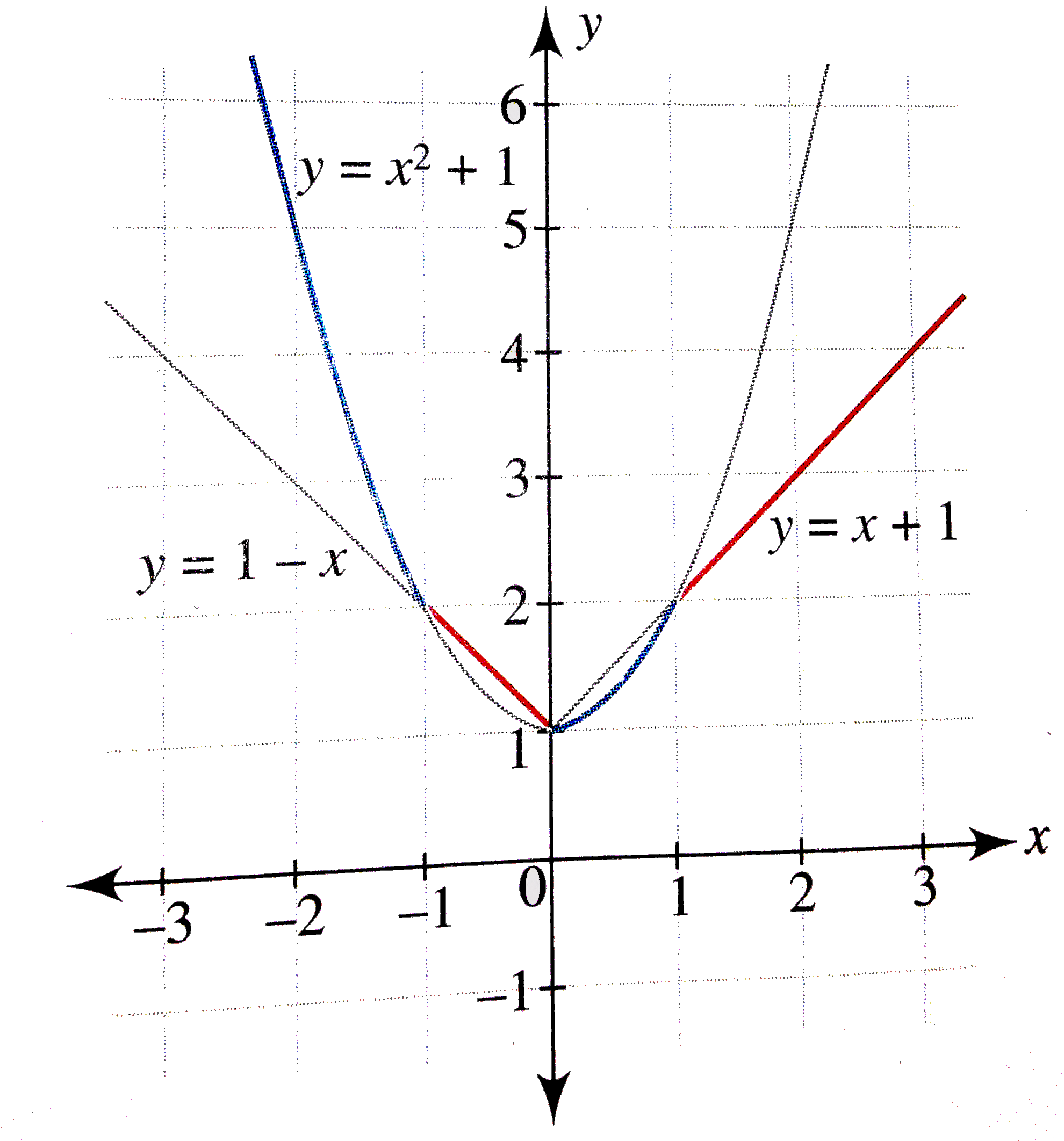
From the graph, the required function is
h(x)=⎧⎪
⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪
⎪⎩x2+1,x∈(−∞,−1)−x+1,x∈[−1,0)x2+1,x∈[0,1)x+1,x∈[1,∞)
which is non-different at x=−1,0and1.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet f:R→(0,∞) and g:R→R be twice differentiable functions such that f" and g" are continuous functions on R. suppose f′(2)=g(2)=0,f(2)≠0 and g'(2)≠0, If limx→2f(x)g(x)f'(x)g'(x)=1 then
View SolutionLet f:R rarr R and g:R rarr R be respectively given by f(x)=|x|+1 and g(x)=x^(2)+1. Define h:R rarr R by h(x)={max{f(x),g(x)},quad if x 0 The number of points at which h(x) is not differentiable is
View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x for all x∈R. Then, h'(1) equals.
View SolutionIf f:R→R,g,R→R be two funcitons, and h(x)=2min{f(x)−g(x),0} then h(x)=
View SolutionLet f:R→R and g:R→R be respectively given by f(x)=|x|+1 and g(x)=x2+1. Define h:R→R by
h(x)={max{f(x),g(x)}ifx≤0min{f(x),g(x)}ifx>0
The number of points at which h(x) is not differentiable is :
View SolutionLet f:R→Randg:R→R is define by f(x)=2x+3andg(x)=3x−2, then find (g∘f)−1(x)
View SolutionLet f:R to R and g:R to R is define by f(x)=2x+3 and g(x)=3x-2 , then find (f circ g)^(-1)(x)
View SolutionIf f:R→R and g:R→R are defined by f(x)=x−[x] and g(x)=[x] is x∈R then f{g(x)}
View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(g(x)))=x for all x∈R. Then, h'(1) equals.
View SolutionLet f:R→Randg:R→R be respectively given by f(x)=|x|+1andg(x)=x2+1. Define h:R→R by h(x)={max{f(x),g(x)},ifx≤0andmin{f(x),g(x)},ifx>0.The number of points at which h(x) is not differentiable is
View SolutionLet f:R→R and h:R→R be differentiable functions such that f(x)=x3+3x+2,g(f(x))=xandh(g(x))=x for all x∈R. Then, h'(1) equals.
View SolutionLetf:R→R and g:R→R be respectively given by f(x)=|x|+1andg(x)=x2+1. Define h:R→R by
h(x)={max{f(x),g(x)}ifx≤0min{f(x),g(x)}ifx>0
The number of points at which h(x) is not differentiable is
View Solution
