Let $f (x) = x + 2 | x + 1 | + 2 | x - 1 |$ . Find the values of $k$ if $f (x) = k$
(i) has exactly one real solution,
(ii) has two negative solutions,
(iii) has two solutions of opposite sign.

Video Solution

Text Solution

Verified by Experts

Let $f (x) = x + 2 | x + 1 | + 2 | x - 1 |$
$y = f (x)$ changes definition at $x = - 1 and x = 1$ .
Since the graph of the function is a straight line in each region $(- \infty, - 1), (- 1, 1) and (1, \infty)$ , we need to check the values at some particular values of x to draw the graphs.
$f (- 2) = - 2 + 2 (1) + 2 (3) = 6$
$f (- 1) = - 1 + 2 (0) + 2 (2) = 3$
$f (1) = 1 + 2 (2) + 2 (0) = 5$
$f (2) = 2 + 2 (3) + 2 (1) = 10$
Thus, we plot the points $(- 2, 6), (- 1, 3), (1, 5) and (2, 10)$ .
Plotting these points and connecting with the straight line, we have the following graph.

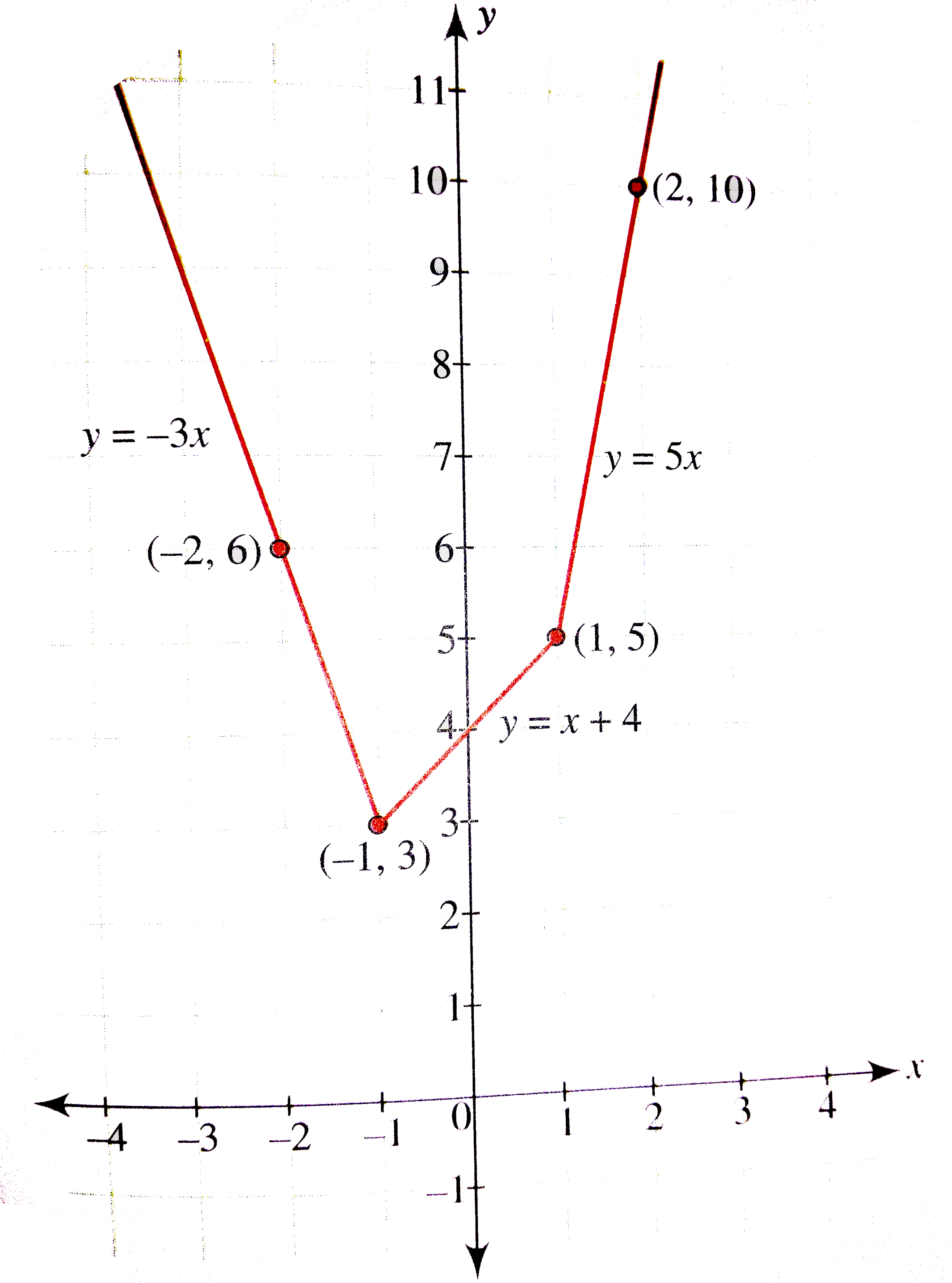
For the equation $f (x) = k$ to have exactly one real root, the line y =k must intersect the graph of $y = f (x)$ at the point $(- 1, 3)$ , hence the value of $k$ is 3.
For the equation $f (x) = k$ to have two negative real roots, the line $y = k$ must intersect the graph of $y = f (x)$ at the point between $y = 3 and y = 4$ , hence the values of k are $(3, 4)$ .
For the equation $f (x) = k$ to have real roots of opposite sign, the line $y = k$ must intersect the graph of $y = f (x)$ above $y = 4$ , hence the values of $k$ are $(4, \infty)$ .

Updated on:21/07/2023

Let $f (x) = \frac{2 | x | - 1}{x - 3}$
Range of the values of 'k' for which $f (x) = k$ has exactly two distinct solutions:
A $(- 2, \frac{1}{3})$
B $(- 2, 1]$
C $(0, \frac{2}{3}]$
D $(- \infty, - 2)$
Minimum integral value of k for which the equation $e^{x} = k x^{2}$ has exactly three real distinct solution,
A1
B2
C3
D4
Let $f (x) = {sin}^{- 1} x - {cos}^{- 1},$ x, then the set of values of k for which of $| f (x) | = k$ has exactly two distinct solutions is :
A $(0, \frac{π}{2}]$
B $(0, \frac{π}{2}]$
C $[\frac{π}{2}, \frac{3 π}{2})$
D $[π, \frac{3 π}{2}]$