Let O be the circumcentre and H be the orthocentre of an acute angled triangle ABC. If , then show that

From the figure, we have
Similarly,
and
Also,
Similarly,
and
Clearly,
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.1
Explore 12 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBook:CENGAGEChapter:PROPERTIES AND SOLUTIONS OF TRIANGLEExercise:Exercise 5.2
Explore 8 Videos
- PROGRESSION AND SERIESBook:CENGAGEChapter:PROGRESSION AND SERIESExercise:ARCHIVES (MATRIX MATCH TYPE )
Explore 1 Video
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBook:CENGAGEChapter:PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEExercise:Question Bank
Explore 32 Videos
Similar Questions
In the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
View SolutionIn the figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that

ar(ΔDOC) = ar(ΔAOB)
View SolutionIn the figur e, diagonals AC and BD of quadrilateral A BCD intersect at 0 such that OB = OD. If AB = CD, then show that

ar(ΔDCB) = ar(ΔACB)
View SolutionIn adjoining figure,AP⊥BC , AD∣∣BC ,then find Ar.(ΔABC):Ar.(ΔBCD)Fig.
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
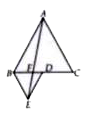
ar(ΔABC) = 2 ar(ΔBEC)
View SolutionP and Q are respectively the mid-points of sides AB and BC of a triangle ABC and R is the mid-point of AP, show that
ar(ΔPRQ) = 1/2 ar(ΔARC)
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
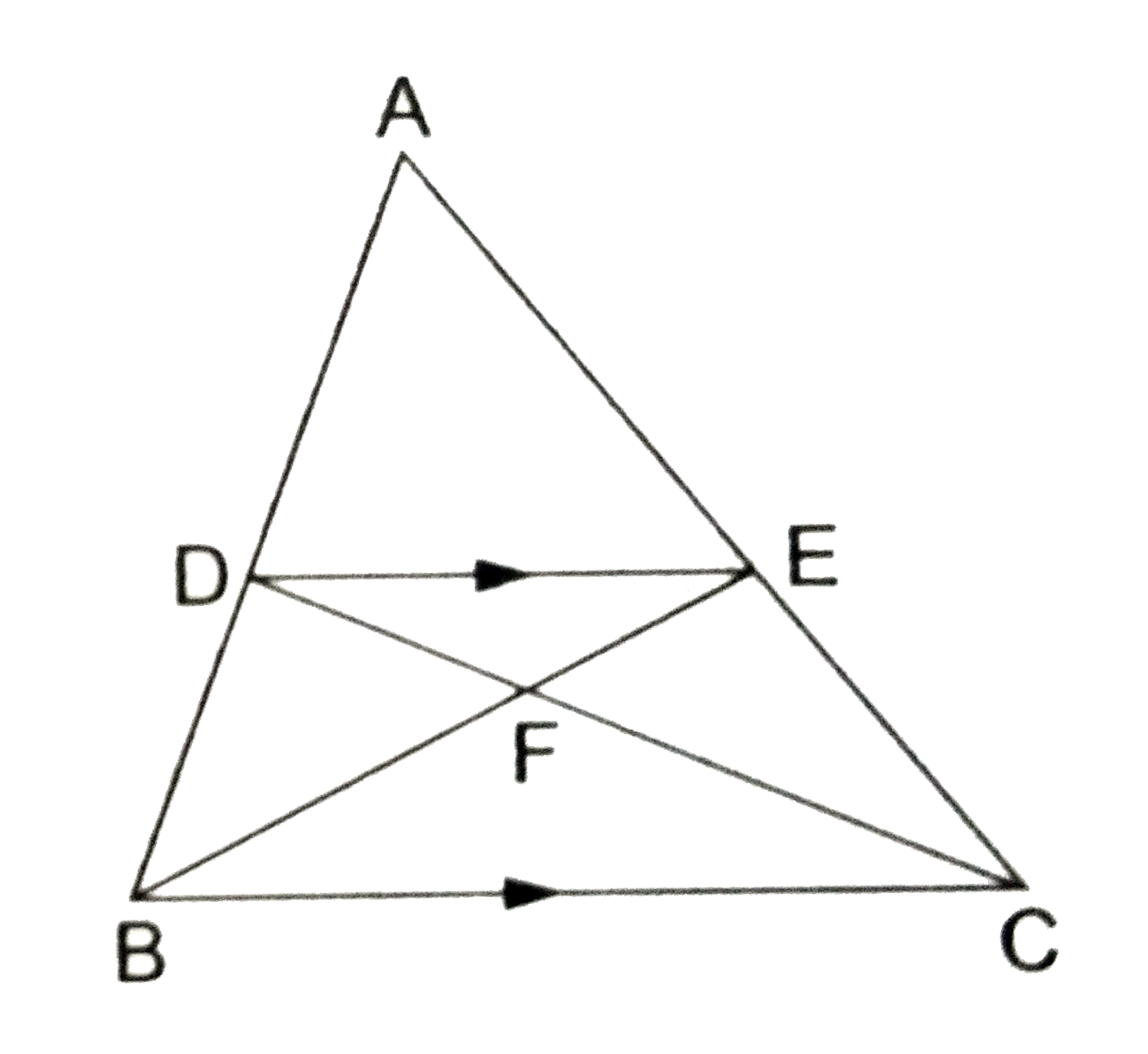
View SolutionIn the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)

View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View Solution
