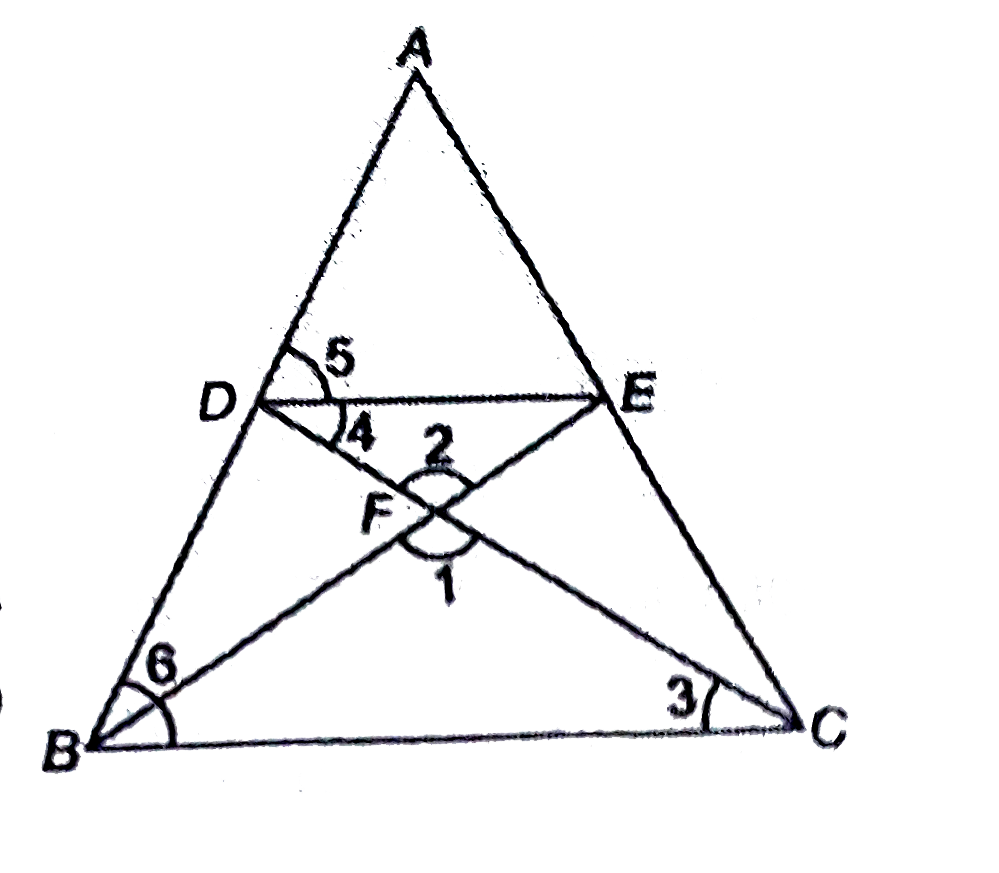
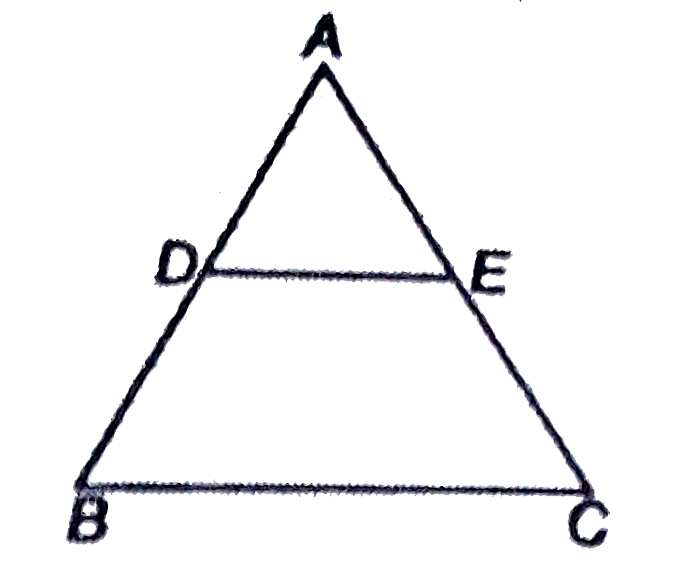
In the given figure DE∣∣BCandAD:DB=5:4
Find the ratio ar(ΔDEF):ar(ΔCFB)
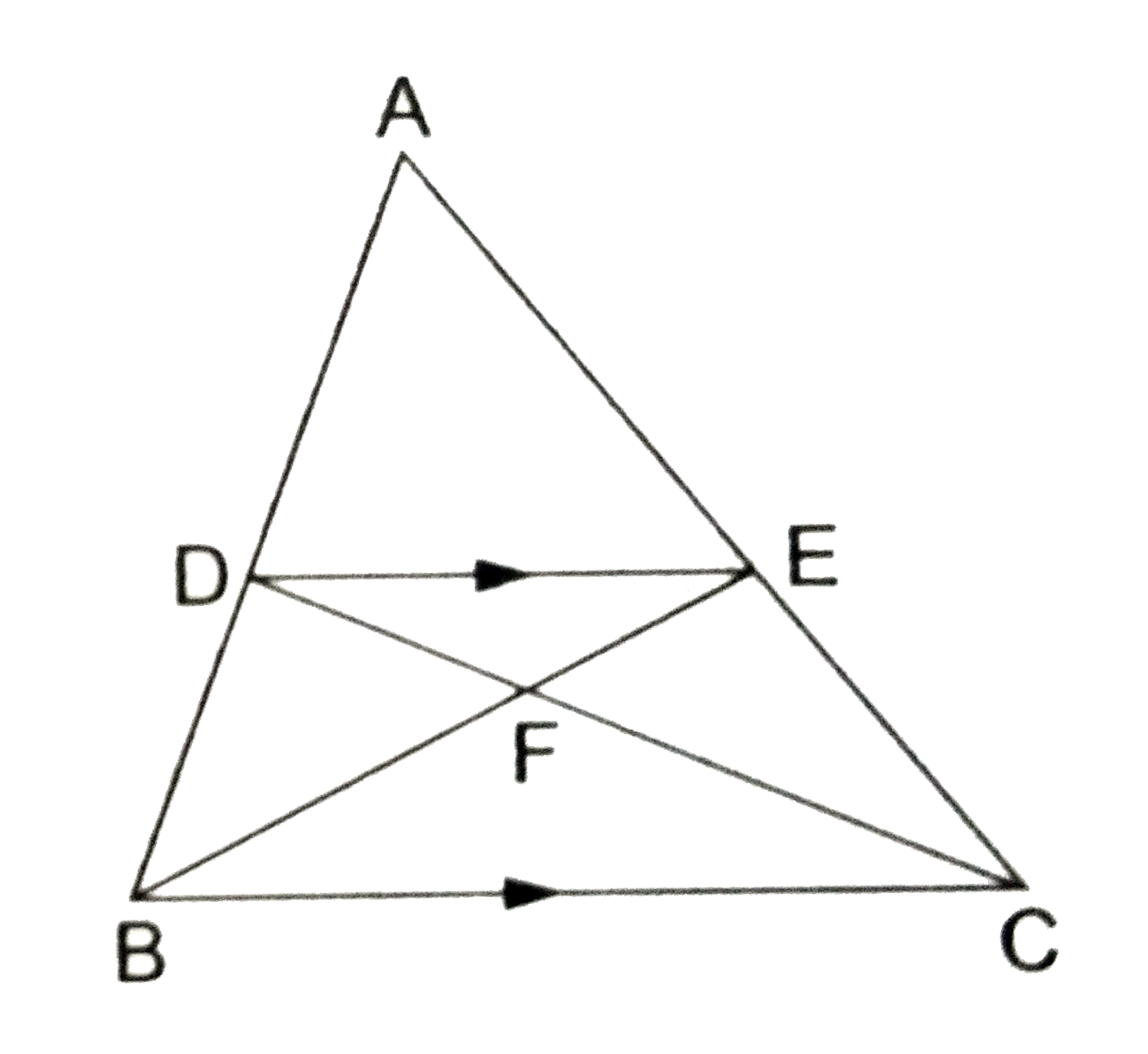
Since DE||BC
In △ADEand△ABC
∠5=∠6 (corresponding angles)
∠aA=∠A (common) ,
△ADE~△ABC (AA corollary)
ADAB=)DEBC
⇒ ADAD+DB=DEBC⇒BCDE=AD+BDAD
⇒ BCDE=1+BDAD⇒BCDE=1+45 (ADBD=54, given )
BCDE=95
DEBC=59 ...(1)
In △DEFand△CFB
∠4=∠3 ( alternate angles as DE||BC)
and ∠2=∠1 ( vertically opposite angles)
△DEF~△CBF (AA corollary)
ar(△DEF)ar(△CBF)=DE2BC2=(59)2 (area ratio theorem)
Hence , ar(△DEF)ar(△CBF)=2581
Topper's Solved these Questions
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Problems From NCERT/ Exemplar
14 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Exercise 6a
24 Videos
- STATISTICS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICS EXERCISE - Revision Exercise Long Answer Questions
4 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Revisions Exercise Long Answer Questions
5 Videos
Similar Questions
In the given figure, DE // BC and AE : EC = 5 : 4. Find :
DE : BC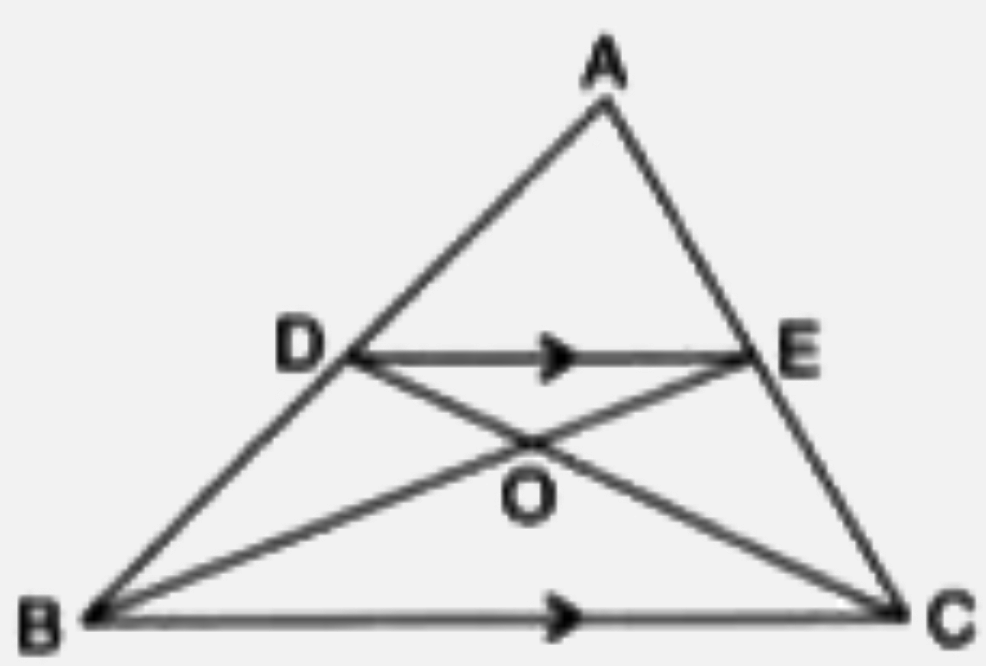
View SolutionIn the given figure , DE //BC and
AD : AB= 2 : 5 Find :
area of ΔADE area of ΔABC
( ii) area of ΔABC area of trapezium DBCE

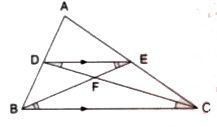
View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 4. Find the ratio :

Area of ΔDEFArea ofΔBFC
View SolutionIn figure, if DE||BC, then find the ratio of ar (ΔADE) and ar(DECB).
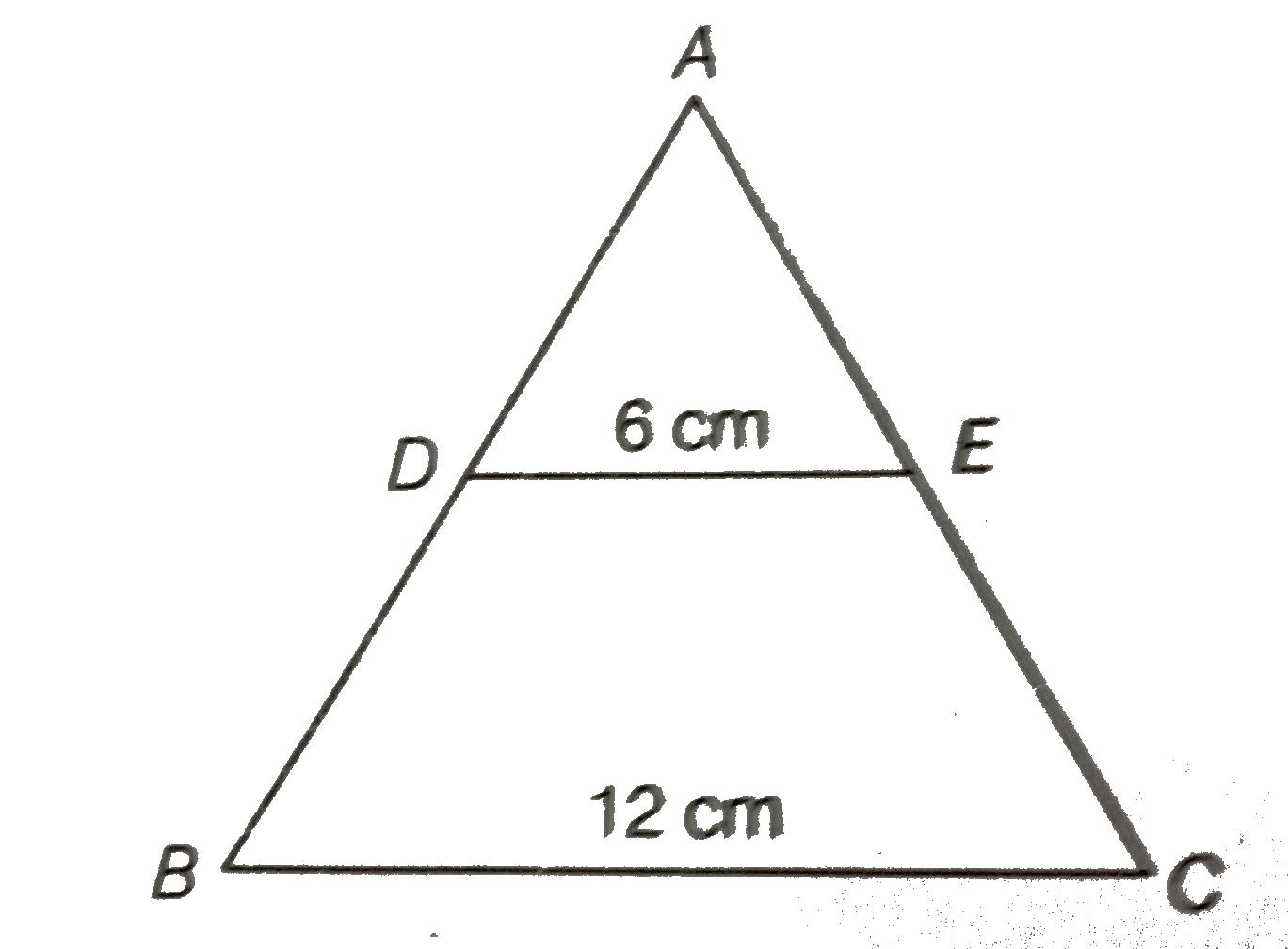
View SolutionIn the given figure, DE||BC and ADDB=23if AE=3.7 cm , find EC.
View SolutionIn the given figure, if DE||AQ and DF||AR. Prove that EF||QR.

View SolutionIn the given figure, DE is parallel to the base BC of triangle ABC and AD: DB = 5: 3. Find the ratio :
ADAB and then DEBC
View SolutionIn the given figure, ABC is a triangle. DE is parallel to BC and ADDB=32

What is the ratio of the areas of ΔDEF and ΔBFC ?
View SolutionIn the given figure, AP||BQ||CR. Prove that ar(ΔAQC)=ar(ΔPBR)

View SolutionIn the given figure, AX:XB=3:5
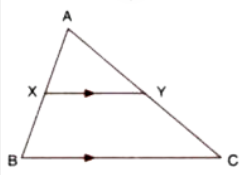
Find :
the ratio between the areas of trapezium XBCY and triangle ABC.
View Solution
