Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:OC.
5/2
6
7/3
4
The correct Answer is:B
Let the position vectors of A, B, C and D be →a,→b,→cand→d, respectively. Then,
OA:CB=2:1
⇒−−→OA=2−−→CB
⇒→a=2(→b−→c) (i)
and OD:AB=1:3
3−−→OD=−−→AB
⇒3→d=(→b−→a)=→b−2(→b−→c) [ using(i)]
=−→b+2→c (ii)
Let OX:XC=λ:1andAX:XD=μ:1
Now, X divides OC in the ratio λ:1. Therefore,
P.VofX=λ→cλ+1 (iii)
X also divides AD in the ratio μ:1. Therefore,
P.V. of X = μ→d+→aμ+1 (iv)
From (iii) and (iv), we get
λ→cλ+1=μ→d+→aμ+1
or (λλ+1)→c=(μμ+1)→d+(1μ+1)→a
or (λλ+1)→c=(μμ+1)(−→b+2→c3)+(1μ+1)2(→b−→c)
[using (i) and (ii)]
or (λλ+1)→c=(6−μ3(μ+1))→b+(2μ3(μ+1)−2μ+1)→c
or (λλ+1)→c=(6−μ3(μ+1))→b+(2μ−63(μ+1))→c
or (6−μ3(μ+1))→b+(2μ−63(μ+1)−λλ+1)→c=→0
or 6−μ3(μ+1)=0and2μ−63(μ+1)−λλ+1=0
( as →band→c are non-collinear )
or μ=6,λ=25
Hence, OX:XC=2:5
Topper's Solved these Questions
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - INTEGER TYPE
8 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - ARCHIVES SUBJECTIVE TYPE
9 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGE ENGLISHCHAPTER - INTRODUCTION TO VECTORS EXERCISE - REASONING TYPE
11 Videos
- INTEGRALSBOOK - CENGAGE ENGLISHCHAPTER - INTEGRALSEXERCISE - All Questions
764 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE ENGLISHCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Archives (Numerical Value type)
2 Videos
Similar Questions
Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:XC.
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal AC.
View SolutionThe side AB of a square ABCD is parallel to the x-axis. Find the slopes of all its sides.

Also, find :
the slope of the diagonal BD.
View SolutionTwo sides of a Rhombus ABCD are parallel to the lines x−y=5 and 7x−y=3. The diagonals intersect at (2,1) then the equations of the diagonals are
View SolutionThe sides AB and AD of a parallelogram ABCD are 2x−y+1=0andx+3y−10=0 respectively and C is the point (−1,−2). Find the equation of the diagonals AC.
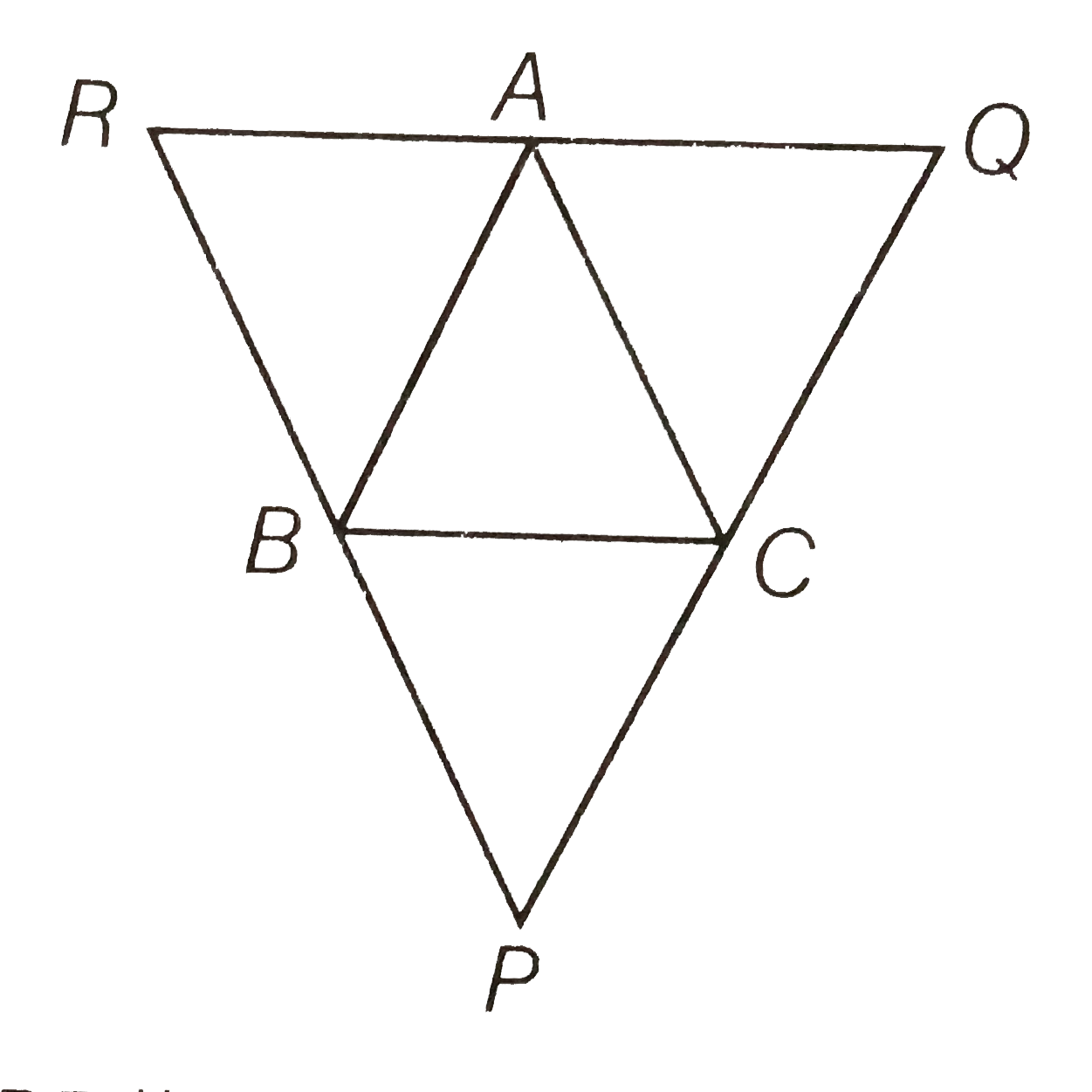
View SolutionThrough A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
View SolutionIn the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
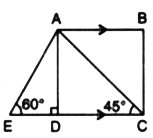
Given that ∠AED=60∘and∠ACD=45∘, calculate :
(i) AB
View SolutionIn the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
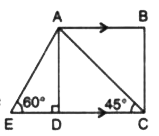
Given that ∠AED=60∘and∠ACD=45∘, calculate :
(iii) AE
View SolutionIn the given figure, AB and EC are parallel to each other. Sides AD and BC are 2 cm each and are perpendicular to AB.
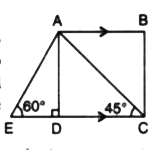
Given that ∠AED=60∘and∠ACD=45∘, calculate :
(ii) AC
View SolutionPerpendicular bisectors of the sides AB and AC of a triangle ABC meet at O.
What is the relation between the distances OA, OB and OC ?
View Solution
