Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel. Also OA:CB=2:1andOD:AB=1:3.

The ratio AXXD is
5/2
6
7/3
4
The correct Answer is:B
Let the position vectors of A, B, C and D be →a,→b,→cand→d, respectively. Then,
OA:CB=2:1
⇒−−→OA=2−−→CB
⇒→a=2(→b−→c) (i)
and OD:AB=1:3
3−−→OD=−−→AB
⇒3→d=(→b−→a)=→b−2(→b−→c) [ using(i)]
=−→b+2→c (ii)
Let OX:XC=λ:1andAX:XD=μ:1
Now, X divides OC in the ratio λ:1. Therefore,
P.VofX=λ→cλ+1 (iii)
X also divides AD in the ratio μ:1. Therefore,
P.V. of X = μ→d+→aμ+1 (iv)
From (iii) and (iv), we get
λ→cλ+1=μ→d+→aμ+1
or (λλ+1)→c=(μμ+1)→d+(1μ+1)→a
or (λλ+1)→c=(μμ+1)(−→b+2→c3)+(1μ+1)2(→b−→c)
[using (i) and (ii)]
or (λλ+1)→c=(6−μ3(μ+1))→b+(2μ3(μ+1)−2μ+1)→c
or (λλ+1)→c=(6−μ3(μ+1))→b+(2μ−63(μ+1))→c
or (6−μ3(μ+1))→b+(2μ−63(μ+1)−λλ+1)→c=→0
or 6−μ3(μ+1)=0and2μ−63(μ+1)−λλ+1=0
( as →band→c are non-collinear )
or μ=6,λ=25
Hence, OX:XC=2:5
Topper's Solved these Questions
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - MATRIX-MATCH TYPE
3 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise (Numerical)
6 Videos
- INTRODUCTION TO VECTORS BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise (Comprehension)
9 Videos
- INTEGRALSBOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises
222 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions
529 Videos
Similar Questions
Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:OC.
View SolutionLet OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:XC.
View Solution
Knowledge Check
In a triangle ABC three forces of magnitudes 3−−→AB,2−−→AC and 6−−→CB are acting along the sides AB, AC and CB respectively . If the resultant meets AC at D, then the ratio DC: AD will be equal to
A1:1B1:2C1:3D1:4
Let OABCD be a pentagon in which the sides OA and CB are parallel and the sides OD and AB are parallel as shown in figure. Also, OA:CB=2:1 and OD:AB=1:3. if the diagonals OC and AD meet at x, find OX:XC.
View SolutionLet ABCD be a quadrilateral with area 18 , side AB parallel to the side CD,andAB=2CD . Let AD be perpendicular to ABandCD . If a circle is drawn inside the quadrilateral ABCD touching all the sides, then its radius is 3 (b) 2 (c) 32 (d) 1
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
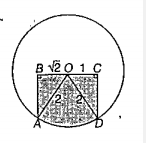
View SolutionIn the following figure the radii (OA and OD) are 2 cm and △ABO and △DCO are right angle triangles. Also, OB=√2 cm and OC = 1 cm. Find the area of the shaded region in the circle.
View SolutionThe following figure shows a trapezium ABCD in which AB is parallel to DC and AD= BC
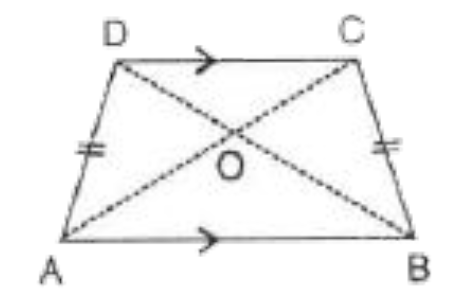
Prove that:
OA = OB and OC= OD
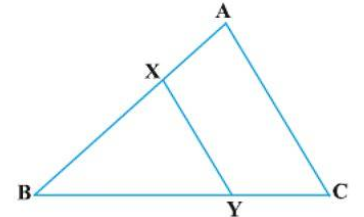
View SolutionIn Figure the line segment XY is parallel to side AC of ΔABCand it divides the triangle into two parts of equal areas. Find the ratio AXAB.
View SolutionA(1,−2)andB(2,5) are two points. The lines OA,OB are produced to CandD respectively, such that OC=2OAandOD=2OB. Find CD.
View Solution
