Let the sequence real numbers satisfies the recurrence relation Then find the Solution in Tamil
The correct Answer is:5
Let
Now
Topper's Solved these Questions
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.3
15 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.4
5 Videos
- LIMITSBOOK - CENGAGECHAPTER - LIMITSEXERCISE - Exercise 2.1
10 Videos
- JEE 2019BOOK - CENGAGECHAPTER - JEE 2019EXERCISE - Chapter 10
9 Videos
- LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSBOOK - CENGAGECHAPTER - LINEAR COMBINATION OF VECTORS, DEPENDENT AND INDEPENDENT VECTORSEXERCISE - DPP 1.2
10 Videos
Similar Questions
Evaluate limx→1(2x−3)(√x−1)2x2+x−3.
View SolutionEvaluate limx→0⎧⎪⎨⎪⎩sinx−x+x36x5⎫⎪⎬⎪⎭.
View SolutionEvaluate: (lim)x→−2+ x2−12x+4
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionThe number of integral values of p for which (p+1)ˆi−3ˆj+pˆk,pˆi+(p+1)ˆj−3ˆk and −3ˆi+pˆj+(p+1)ˆk are linearly dependent vectors is q
View SolutionLet the sequence {bn} real numbers satisfies the recurrence relation bn+1=13(2bn+125bn2),bn≠0. Then find the (lim)n→∞bn.
View Solutionlet {a_n},{b_n},{c_n} be sequences such that (1) a_n+b_n+c_n=2n+1 , (2) a_nb_n+b_nc_n+c_na_n=2n-1 , (3) a_nb_nc_n=-1 , (4) a_n oo) (na_n)
View SolutionLet the sequence {bn} real numbers satisfies the recurrence relation bn+1=13(2bn+125bn2),bn≠0. Then find the (lim)n→∞bn.
View SolutionIf an=34−(34)2+(34)3+...(−1)n−1(34)n and bn=1−an, then find the minimum natural number n, such that bn>an
View SolutionLet f(x)=a0+a1x+a2x2+...+anxn and f(x)1−x=b0+b1x+b2x2+...+bnxn , then a. bn+bn−1=an b. bn−bn−1=an c. bnbn−1=an d. none of these
View SolutionIf an and bn are positive integers and an+√2bn=(2+√2)n,then(lim)n→∞(anbn)= a. 2 b. √2 c. e√2 d. e2
View SolutionLet the sequence <bn> of real numbers satisfy the recurrence relation bn+1=13(2bn+125b2n),bn≠0. Then find limn→o0bn.
View SolutionProve that if the sequence {an/bn}{bn>0} is monotonic, then the sequence. {a1+a2+.....+anb1+b2+.....+bn} will also be monotonic.
View SolutionComplete the following statements.
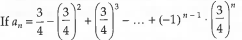 and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
and bn=1−an then the smallest natural number n0, such that bn>anVntn>n0 is
View SolutionLet An=(34)−(34)2+(34)3+.....+(−1)n−1(34)n , B_n = 1 - A_n . Find a least odd natural number n0, so that Bn>An∀n≥n0.
View SolutionLet the sequence {bn} real numbers satisfies the recurrence relation bn+1=13(2bn+125(bn)2),bn≠0. Then find the (lim)n→∞bn.
View Solution
