M and N are point on sides QR and PQ respectively of △PQR, right-anggled at Q. Prove that :
4PM2=4PQ2+QR2.
Step by step video & image solution for M and N are point on sides QR and PQ respectively of /_\ PQR, right-anggled at Q. Prove that : 4PM^(2)= 4PQ^(2)+QR^(2). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEORAMBOOK - ICSECHAPTER - PYTHAGORAS THEORAMEXERCISE - QUESTIONS
9 Videos
- PYTHAGORAS THEORAMBOOK - ICSECHAPTER - PYTHAGORAS THEORAMEXERCISE - QUESTIONS
9 Videos
- MID-POINT THEOREMBOOK - ICSECHAPTER - MID-POINT THEOREMEXERCISE - 4 MARKS QUESTION
15 Videos
- PYTHAGORAS THEOREMBOOK - ICSECHAPTER - PYTHAGORAS THEOREMEXERCISE - 4 MARKS QUESTIONS
9 Videos
Similar Questions
M and N are mid point on sides QR and PQ respectively of △PQR, right-anggled at Q. Prove that :
4PM2=4PQ2+QR2.
View SolutionM and N are point on sides QR and PQ respectively of △PQR, right-angled at Q. Prove that :
PM2+RN2=PR2+MN2
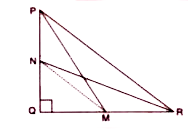
View SolutionM and N are mid- point on sides QR and PQ respectively of △PQR, right-anggled at Q. Prove that :
PM2+RN2=5MN2.
View SolutionM and N are the mid-points of the sides QR and PQ respectively of a ΔPQR, right-angled at Q. Prove that :
(i) PM2+RN2=5MN2
(ii) 4PM2=4PQ2+QR2
(iii) 4RN2=PQ2+4QR2
(iv) 4(PM2+RN2)=5PR2
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View SolutionIn a triangle PQR, L and M are two points on the base QR, such that ∠LPQ=∠QRP and ∠RPM=∠RQP. Prove that:
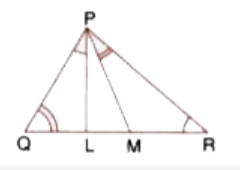
PQ2=QR×QL
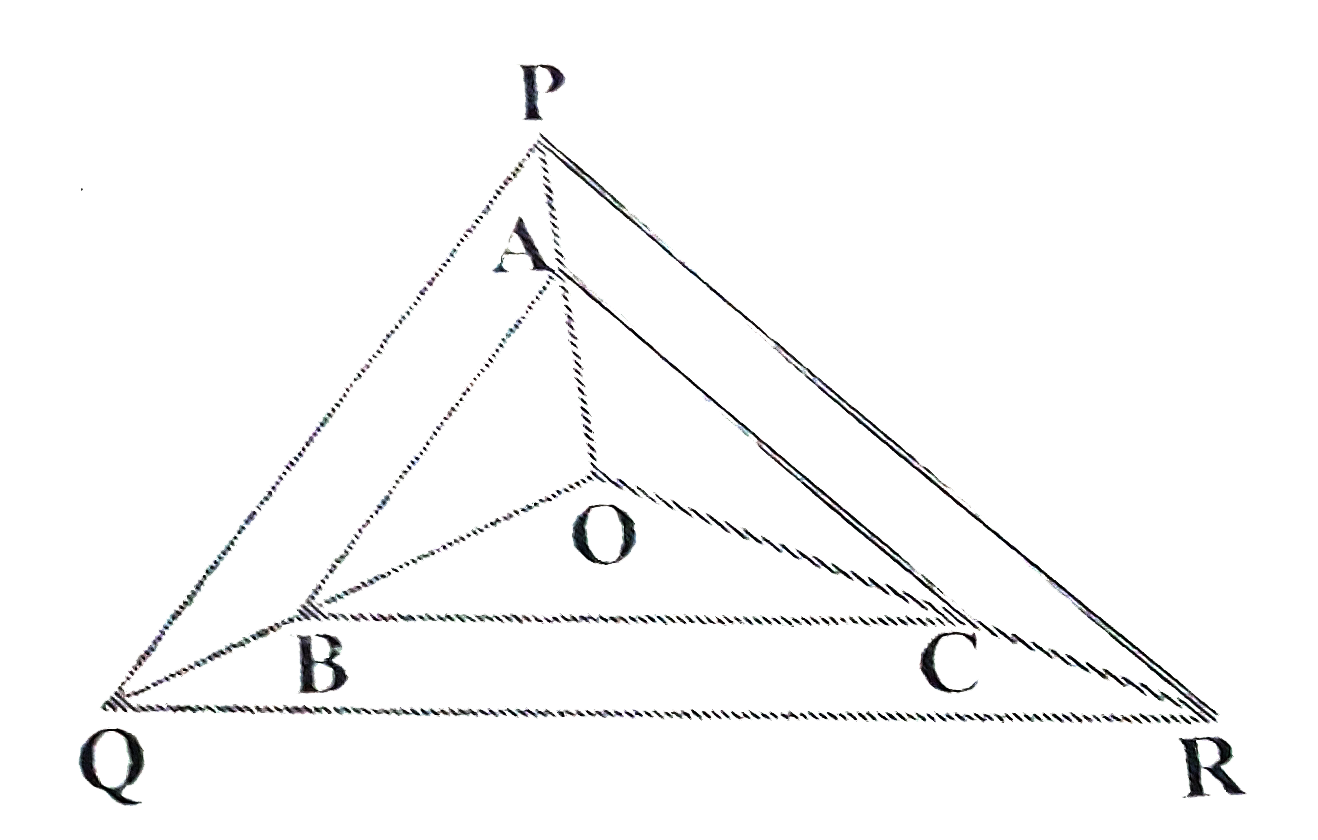
View SolutionIn figure A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
View SolutionABCD is a square. P, Q and Rare the points on AB, BC and CD respectively, such that AP = BQ = CR. Prove that:
PQ = QR
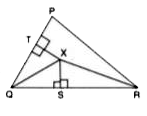
View SolutionIn the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS⊥QRandXT⊥PQ, prove that :
ΔXTQ≅ΔXSQ
View SolutionIn the adjoining figure, ΔPQR is formed by the sides PQ, QR and RP which are drawn parallel to sides AB,BC and CA respectively of ΔABC. Prove that
PQ+QR+RP=2(AB+BC+CA).

View Solution
