O' is any point on diagonal AC of a parallelogram ABCD. Prove that :
area of
To prove that the area of triangle AOD is equal to the area of triangle AOB when O is any point on diagonal AC of parallelogram ABCD, we can follow these steps:
1. Given Information:
- Let ABCD be a parallelogram.
- O is any point on diagonal AC.
2. Properties of Parallelogram:
- The diagonal AC divides the parallelogram ABCD into two triangles: triangle ABC and triangle ADC.
- The area of triangle ABC is equal to the area of triangle ADC because the diagonal of a parallelogram divides it into two equal areas.
3. Construct Perpendiculars:
- Draw perpendiculars from points B and D to line AC. Let these perpendiculars meet AC at points M and N, respectively.
- Thus, BM is the height from B to AC and DN is the height from D to AC.
4. Area of Triangles:
- The area of triangle ABC can be expressed as:
Area of △ABC=12×AC×BM
- The area of triangle ADC can be expressed as:
Area of △ADC=12×AC×DN
5. Equating Areas:
- Since the areas of triangles ABC and ADC are equal, we have:
12×AC×BM=12×AC×DN
- This implies that:
BM=DN
6. Area of Triangles AOD and AOB:
- Now, consider triangles AOD and AOB.
- The area of triangle AOD can be expressed as:
Area of △AOD=12×OA×DN
- The area of triangle AOB can be expressed as:
Area of △AOB=12×OA×BM
7. Substituting Equal Heights:
- Since we established that BM=DN, we can replace DN in the area of triangle AOD:
Area of △AOD=12×OA×BM
8. Conclusion:
- Therefore, we have:
Area of △AOD=Area of △AOB
- This completes the proof that the area of triangle AOD is equal to the area of triangle AOB.
- Let ABCD be a parallelogram.
- O is any point on diagonal AC.
- The diagonal AC divides the parallelogram ABCD into two triangles: triangle ABC and triangle ADC.
- The area of triangle ABC is equal to the area of triangle ADC because the diagonal of a parallelogram divides it into two equal areas.
- Draw perpendiculars from points B and D to line AC. Let these perpendiculars meet AC at points M and N, respectively.
- Thus, BM is the height from B to AC and DN is the height from D to AC.
- The area of triangle ABC can be expressed as:
Area of △ABC=12×AC×BM
- The area of triangle ADC can be expressed as:
Area of △ADC=12×AC×DN
- Since the areas of triangles ABC and ADC are equal, we have:
12×AC×BM=12×AC×DN
- This implies that:
BM=DN
- Now, consider triangles AOD and AOB.
- The area of triangle AOD can be expressed as:
Area of △AOD=12×OA×DN
- The area of triangle AOB can be expressed as:
Area of △AOB=12×OA×BM
- Since we established that BM=DN, we can replace DN in the area of triangle AOD:
Area of △AOD=12×OA×BM
- Therefore, we have:
Area of △AOD=Area of △AOB
- This completes the proof that the area of triangle AOD is equal to the area of triangle AOB.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (very Short Answer Questions)10videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (short Answer Questions)10videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Problems From NCERT/exemplar12videos
AREA OF PARALLELOGRAMS AND TRIANGLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
Similar Questions
O' is an interior point of a parallelogram ABCD. Prove that :
area of ΔAOB+ area of ΔCOD= area of ΔAOD+ area of ΔBOCView SolutionIn the adjoning figure, ABCD is a parallelogram. Prove that : area of ΔBPC= area of ΔDPQ
 View Solution
View SolutionO is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(△OAB)=ar(△OBC)
View SolutionIn triangle ABC, D is mid-point of AB and P is any point on BC. If CQ parallel to PD meets AB at Q, prove that: 2× area (ΔBPQ)= area (ΔABC)
View SolutionABCD is a parallelogram. Find the ratio of the area of Δ ABC to the area of the parallelogram ABCD.
View SolutionP is any point inside a parallelogram ABCD. Prove that :
Area (ΔAPB)+Area(ΔCPD)
=Area(ΔAPD)+Area(ΔBPC)View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionIf P is any point in the interior of a parallelogram ABCD, then prove that area of the triangle APB is less than half the area of parallelogram.
View SolutionIn the adjoining figure, ABCD is a quadrilateral in which AD∣∣BC. AC and BD intersect each other at point 'O'. Prove that:
area of ΔCOD= area of ΔABO
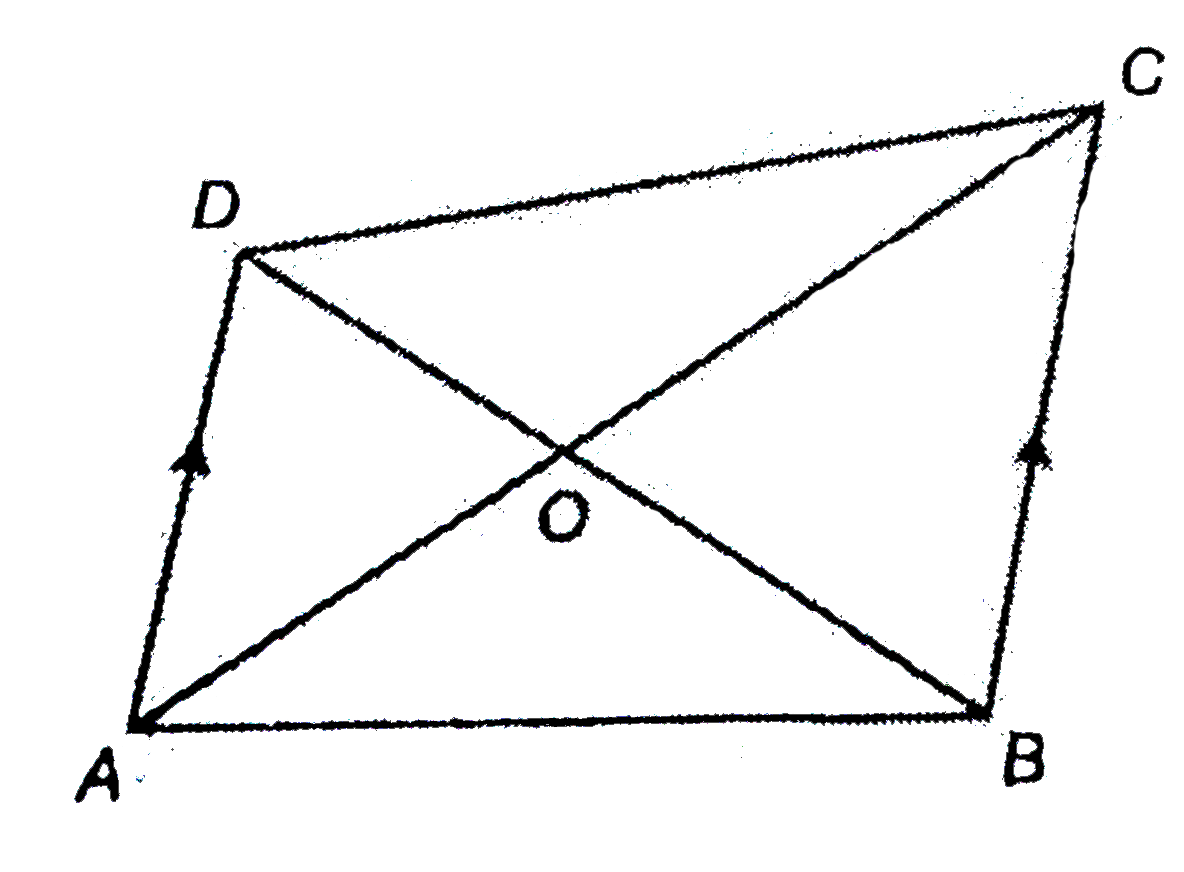 View Solution
View SolutionIn the figure, ABCD is a quadrilateral. A line DP drawn parallel to diagonal AC from point D, meet BC produced at P. Prove that:
are of ΔABP= area of □ABCD
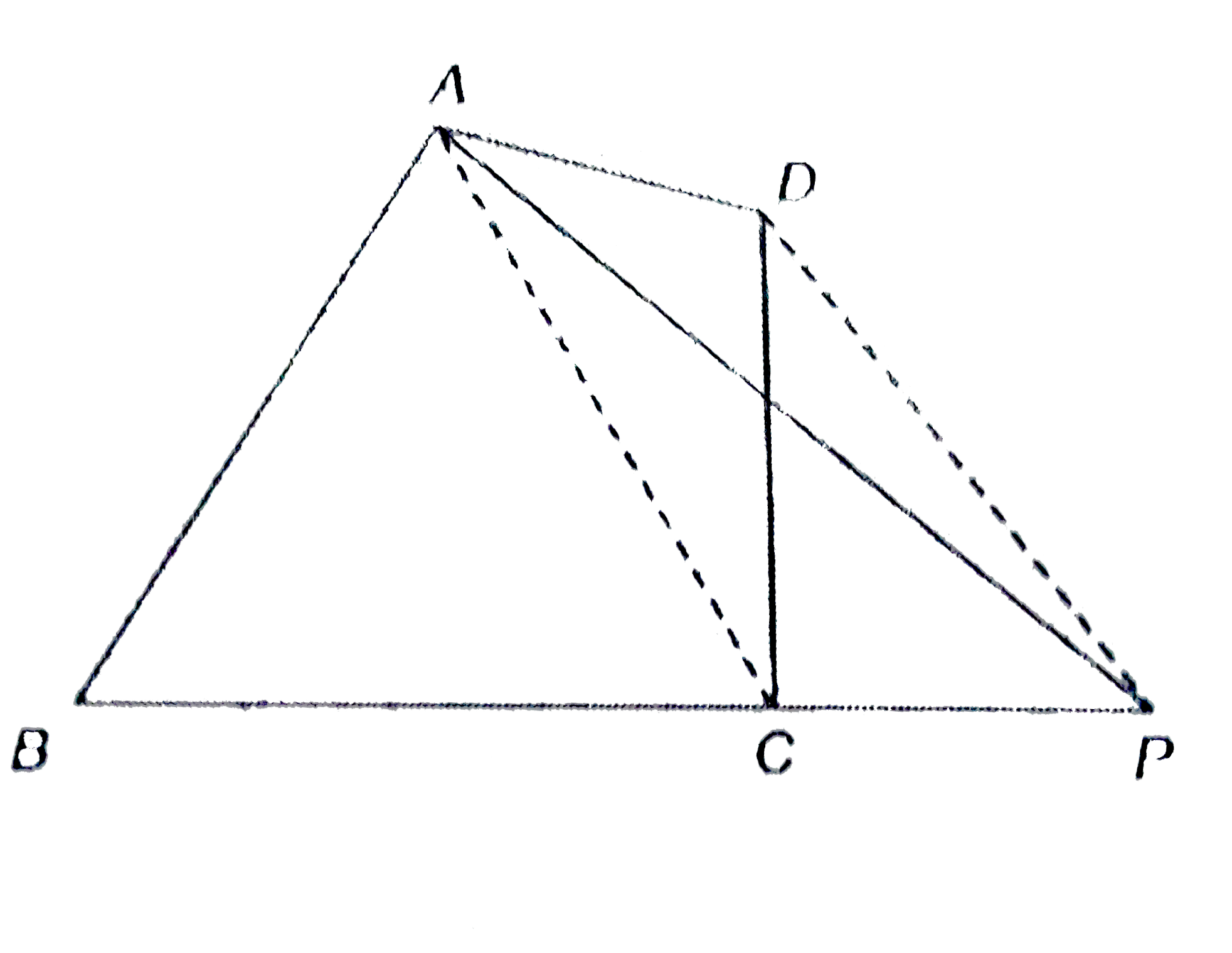 View Solution
View Solution
