P and Q are the points of trisection of the diagonal BD of a parallelogram ABCD. Prove that CQ is parallel to AP. Prove also that AC bisects PQ.
Since diagonals of a parallelogram bisect each other.
Therefore,OA=OCand OB=OD
Since Pand Q are points of trisection of BD.
BP=PQ=QD
OB=ODand BP=QD
⇒OP−BP=OD−QD
⇒OP=OQ
Thus, in quadrilateral APCQ, we have
OA=OCand OP=OQ
Diagonals of quadrilateral APCQ bisect each other
⇒APCQ is a parallelogram
Hence, AP∥CQ
Topper's Solved these Questions
Similar Questions
O is any point on the diagonal BD of the parallelogram ABCD. Prove that ar(OAB)=ar(OBC)
View SolutionIn Figure, AN and CP are perpendicular to the diagonal BD of a parallelogram ABCD. Prove that : ADN≅CBP (ii) AN=CP
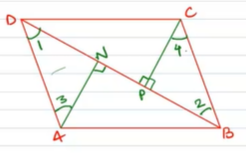 View Solution
View SolutionIn a parallelogram ABCD, points P and Q are points of trisection of diagonal BD. Prove that CQ is parallel to AP.
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionIf P and Q are the mid points of the sides AB and CD of a parallelogram ABCD, prove that DP and BQ cut the diagonal AC in its points of trisection which are also the points of trisection of DP and BQ respectively.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
 View Solution
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View Solution

