P is the mid-point of the side CD of a parallelogram ABCD. A line through C parallel to PA intersects AB at Q and DA produced at R. Prove that DA = AR and CQ = QR.
Given In a parallelogram ABCD, P is the mid-point of DC.
To prove DA=AR and CQ=QR
Proof ABCD is a parallelogram.
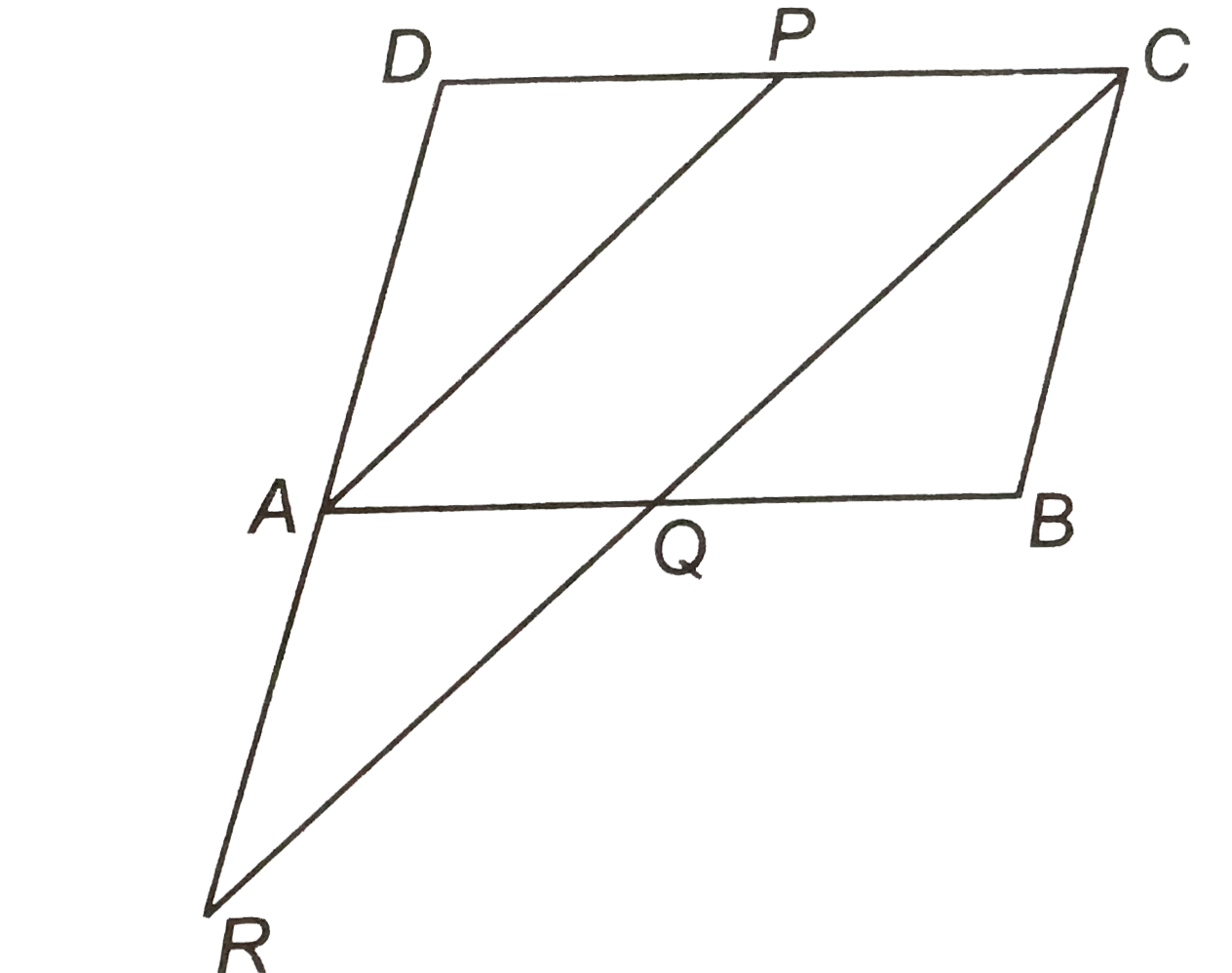
∴ BC=ADandBC∣∣AD
Also, DC=ABandDC∣∣AB
Since, P is the mid-point of DC.
∴ DP=PC=12DC
Now, QC||APandPC||AQ
So, APCQ is a parallelogram.
∴ AQ=PC=12DC
=12AB=BQ [∵DC=AB]...(i)
Now, in ΔAQR and ΔBQC, AQ=BQ [from Eq. (i)]
∠AQR=∠BQC [vertically opposite angles]
and ∠ARQ=∠BCQ [Alternate interior angles]
∴ ΔAQR≅ΔBQC [by AAS congruence rule] ltBrgt ∴ AR=BC [by CPCT rule]
But BC=DA
∴ AR=DA
Also, CQ=QR [ by CPCT rule]
Hence proved.
Topper's Solved these Questions
Similar Questions
P is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionP is the mid-point of side AB of parallelogram ABCD. A line drawn from B parallel to PD meets CD at Q and AD produce at R. Prove that :
(i) AR = 2BC (ii) BR= 2BQView Solution
Knowledge Check
- Question 1 - Select One
E is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
P is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
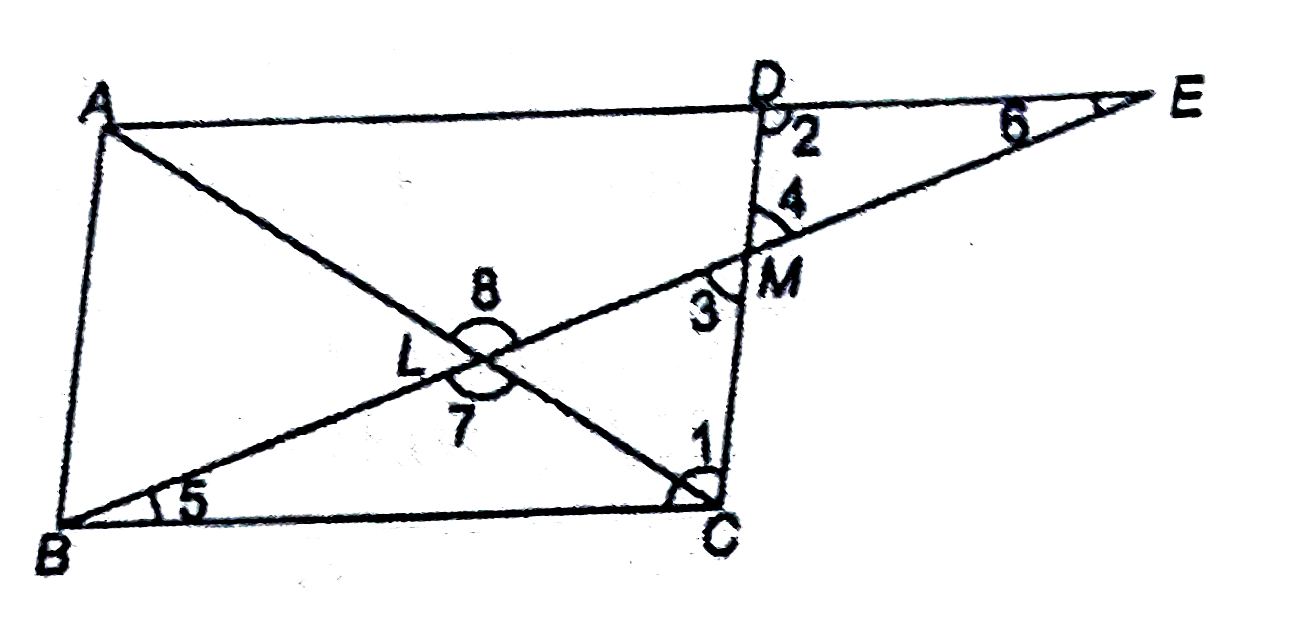
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD , the line BM is drawn intersecting AC at LandAD produced at E . Prove that EL=2BL.
View SolutionThrough the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn, intersecting AC in L and AD produced in El. Prove that EL= 2BL
 View Solution
View SolutionABCD is a parallelogram . The circle passing through the vertices. A, B and C intersects CD (or CD produced) at E. Prove that AE=AD.
View SolutionABCD is a parallelogram. The circle through A, B and C intersect CD (produced ifnecessary) at E. Prove that AE = AD.
View SolutionIn △ ABC, the bisectors of ∠B and ∠ C intersect at I. A line drawn through I and parallel to BC intersects AB at P and AC at Q. Prove that PQ = BP + CQ.
View SolutionABCD is a parallelogram. The circle through A,BandC intersects CD produced at E, prove that AE=AD.
View Solution

