P is the variable point on the circle with center at C.CA and CB are perpendiculars from C on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle PAB is a circle with center at the centroid of triangle CAB and radius equal to the one-third of the radius of the given circle.
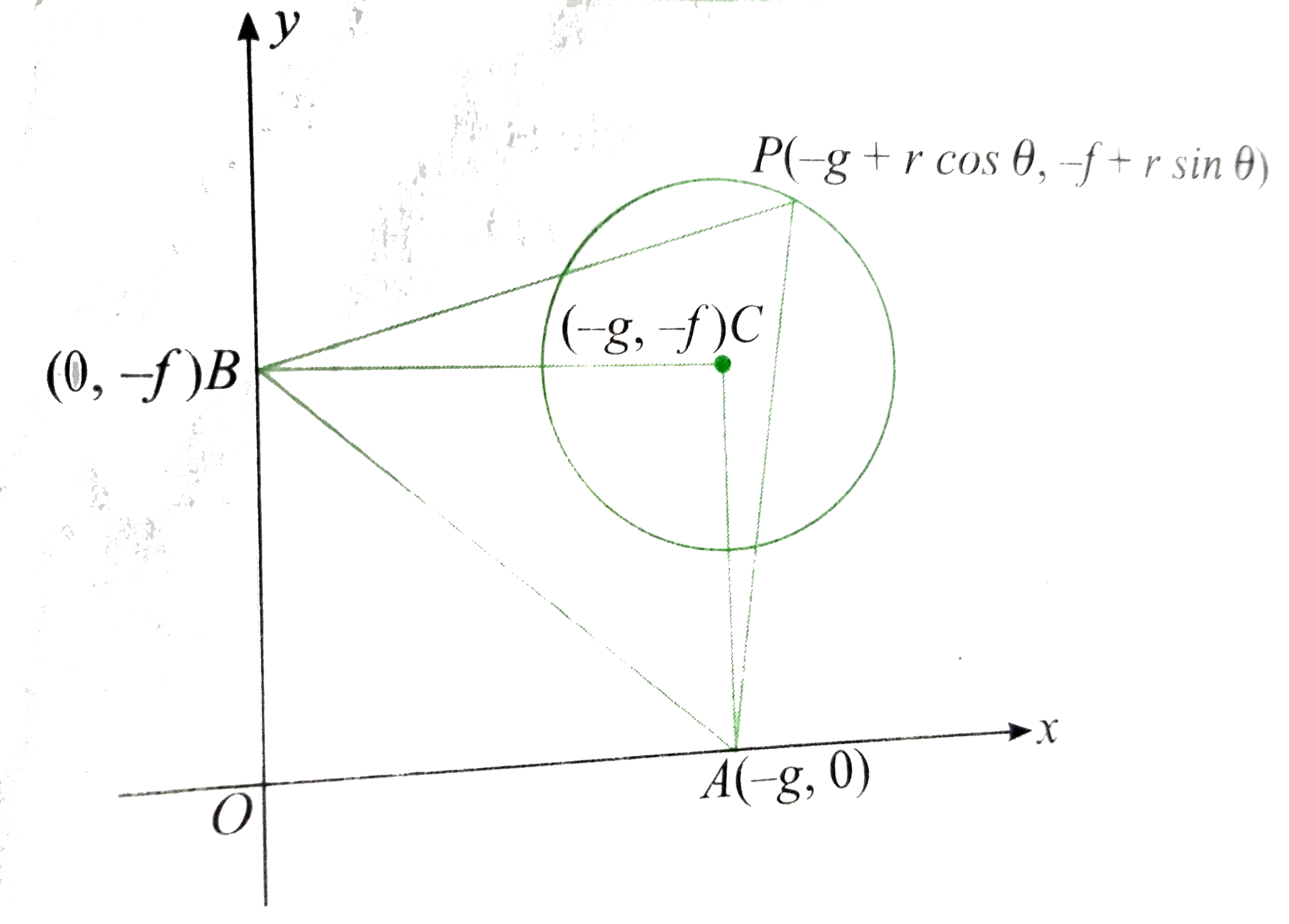
Let the circle be x2+y2+2gx+2fy+c=0.
Let the centroid of triangle PAB be (h,k). ltBRgt ∴3h=2g+rcosθ
and 3k=−2f+rsinθ
⇒(2h+2g)2+(3k+2f)2=r2
⇒(x+2g/3)2+(y+2/3)2=r2/9
This is the required locus which is a circle.
Centre of the circle is (−2g/3,−2f/3) which is centroid of the triangle CAB and radius (r/3) which is one-third of the radius of the given circle.
Topper's Solved these Questions
Similar Questions
P is the variable point on the circle with center at C.CA and CB are perpendiculars from C on the x- and the y-axis, respectively. Show that the locus of the centroid of triangle PAB is a circle with center at the centroid of triangle CAB and radius equal to the one-third of the radius of the given circle.
View SolutionA circle of radius 'r' passes through the origin O and cuts the axes at A and B,Locus of the centroid of triangle OAB is
View Solution
Knowledge Check
A plane a constant distance p from the origin meets the coordinate axes in A, B, C. Locus of the centroid of the triangle ABC is
Ax2+y2+z2=p2Bx−2+y−2+z−2=9p−2Cx−1+y−1+z−1=3p−1Dnone of these
If the intercepts of the variable circle on the x- and yl-axis are 2 units and 4 units, respectively, then find the locus of the center of the variable circle.
View Solutioncircle of radius 3k passes through (0,0) and cuts the axes in A and B then the locus of centroid of triangle OAB is
View SolutionA circle of radius 3k passes through (0.0) and cuts the axes in A and B then the locus of centroid of triangle OAB is
View SolutionA=(1,2),B(3,4) and the locus of C is 2x+3y=5 then the locus of the centroid of ΔABC is
View SolutionIf a circle of constant radius 3c passes through the origin and meets the axes at AandB , prove that the locus of the centroid of △ABC is a circle of radius 2c
View SolutionType I: A point P is 13cm from the center of the circle. The length of the tangent drawn from P to the circle is 12 cm . Find the radius of the circle ?
View SolutionProve that the locus of a point which moves such that the sum of the square of its distances from the vertices of a triangle is constant is a circle having centre at the centroid of the triangle.
View Solution
