PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T . Find the length TP .
To find the length TP where P and Q are points on a circle with radius 5 cm and chord PQ of length 8 cm, we can follow these steps:
Step 1: Identify the given information
- Radius of the circle r=5 cm
- Length of the chord PQ=8 cm
Step 2: Find the distance from the center of the circle to the chord
Let O be the center of the circle, and let R be the midpoint of the chord PQ. Since R is the midpoint, we have:
PR=RQ=PQ2=82=4 cm
Step 3: Use the Pythagorean theorem
In triangle OPR, we can apply the Pythagorean theorem:
OP2=OR2+PR2
Where:
- OP=5 cm (radius)
- PR=4 cm
Let OR be h:
52=h2+42
25=h2+16
h2=25−16=9
h=3 cm
Step 4: Find the length of the tangent TP
In triangle TPR, we again apply the Pythagorean theorem:
TP2=PR2+RT2
Where RT is the distance from point T to point R. Since OT is the angle bisector and is perpendicular to PQ, we can find OT using the Pythagorean theorem in triangle OTR:
OT2=TP2+OR2
Here, OR=3 cm and OT=OP=5 cm:
52=TP2+32
25=TP2+9
TP2=25−9=16
TP=√16=4 cm
Final Answer
The length TP is 4 cm.
---
- Radius of the circle r=5 cm
- Length of the chord PQ=8 cm
Let O be the center of the circle, and let R be the midpoint of the chord PQ. Since R is the midpoint, we have:
PR=RQ=PQ2=82=4 cm
In triangle OPR, we can apply the Pythagorean theorem:
OP2=OR2+PR2
Where:
- OP=5 cm (radius)
- PR=4 cm
52=h2+42
25=h2+16
h2=25−16=9
h=3 cm
In triangle TPR, we again apply the Pythagorean theorem:
TP2=PR2+RT2
Where RT is the distance from point T to point R. Since OT is the angle bisector and is perpendicular to PQ, we can find OT using the Pythagorean theorem in triangle OTR:
OT2=TP2+OR2
Here, OR=3 cm and OT=OP=5 cm:
52=TP2+32
25=TP2+9
TP2=25−9=16
TP=√16=4 cm
The length TP is 4 cm.
Topper's Solved these Questions
Similar Questions
Knowledge Check
PQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A163 cmB203 cmC185 cmD196 cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cmPQ is a chord of length 8 cm, of a circle with centre O and of radius 5 cm. The tangents at P and Q intersect at a point T. The length of TP is
A203cmB214cmC103cmD154cm
AB is a chord of length 24cm of a circle of radius 13cm .The tangents at A and B intersect at a point C. Find the length AC
View SolutionIn Fig. 10.59, AB is a chord of length 16cm of a circle of radius 10cm. The tangents at A and B intersect at a point P . Find the length of PA . (FIGURE)
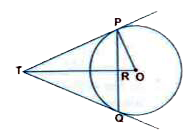
View SolutionIn Fig , PQ is a chord of length 16 cm, of a radius 10 cm . The tangents at P and Q intersect at a point T. Find the length of TP.
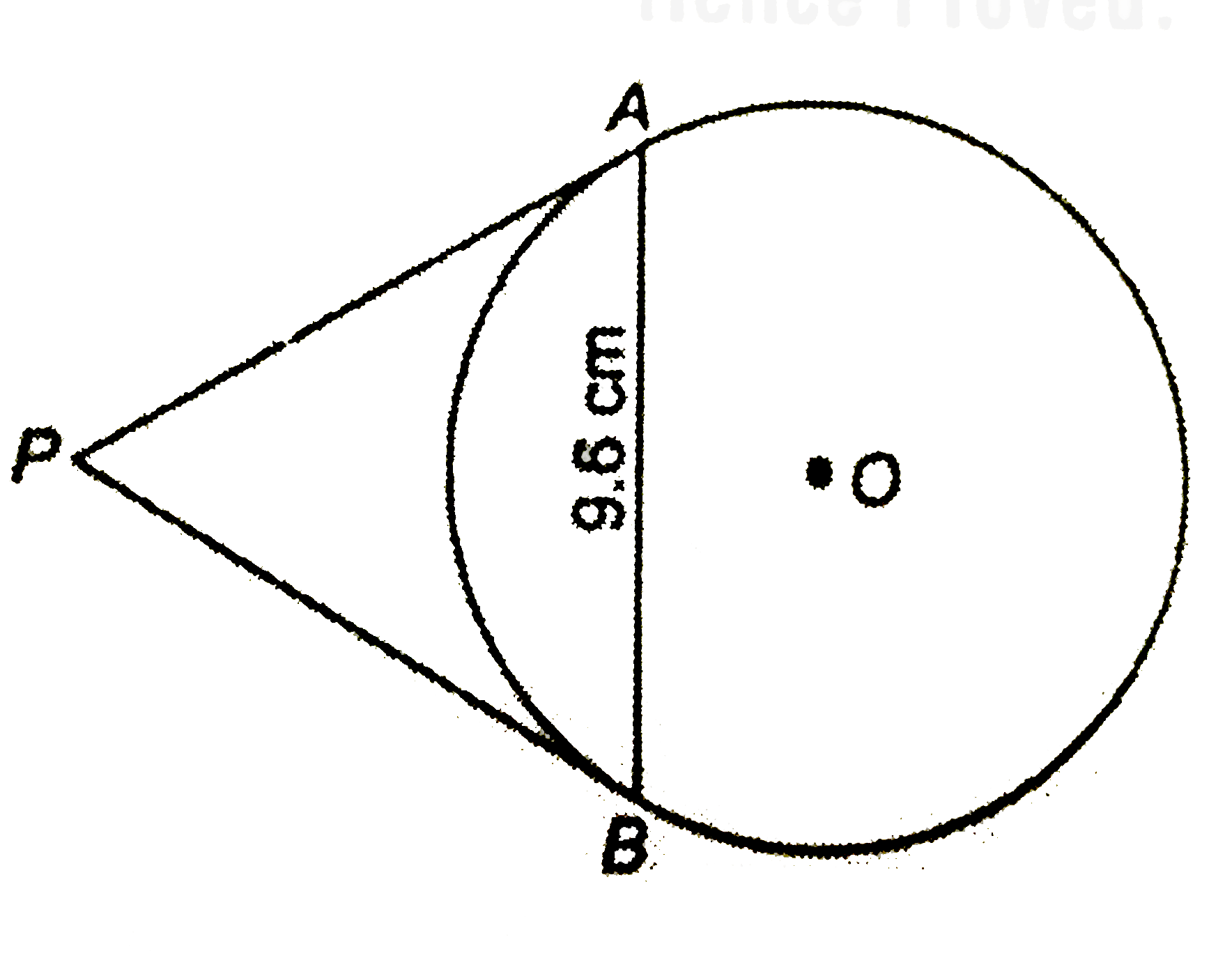
View SolutionIn the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
View SolutionPQ is chord of length 6 cm of a circle of radius 5 cm. Tangents to the circle at P and Q meet at T. Length of TP is
View Solution
