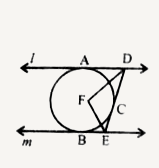
In Fig. 10.32, l and m are two parallel tangents at A and B . The tangent at C makes an intercept DE between l and m . Prove that ∠DFE=90o .
To prove that the angle ∠DFE=90∘, we will follow these steps:
Step 1: Identify the given elements
We have two parallel tangents l and m at points A and B respectively. A tangent at point C intersects the parallel lines at points D and E.
Step 2: Understand the properties of tangents and angles
Since l and m are parallel, the angles formed by the tangent at point C with the tangents at points A and B can be analyzed. The angle ∠ADE and ∠BED are formed by the tangent at C with the tangents at points A and B.
Step 3: Use the property of angles formed by a transversal
By the properties of parallel lines, we know that:
∠ADE+∠BED=180∘
This is because D and E are points on the transversal line CE that intersects the parallel lines l and m.
Step 4: Establish congruence of triangles
Now, consider triangles ADF and CDF:
- AD and DC are tangents from point D to the circle, hence AD=DC.
- AF=CF (both are radii of the circle).
- DF=DF (common side).
By the Side-Side-Side (SSS) congruence criterion, we can conclude that:
△ADF≅△CDF
Thus, we have:
∠ADF=∠CDF
Step 5: Repeat for the other triangle
Similarly, consider triangles BEF and CEF:
- BE and CE are also tangents from point E to the circle, hence BE=CE.
- BF=CF (both are radii of the circle).
- EF=EF (common side).
By the SSS congruence criterion, we can conclude that:
△BEF≅△CEF
Thus, we have:
∠BEF=∠CEF
Step 6: Relate the angles
Now, we can express the angles ∠ADE and ∠BED in terms of the angles we found:
∠ADE=∠ADF+∠CDF=2⋅∠ADF
∠BED=∠BEF+∠CEF=2⋅∠BEF
Step 7: Set up the equation
Since we know:
∠ADE+∠BED=180∘
Substituting the expressions we found:
2⋅∠ADF+2⋅∠BEF=180∘
Dividing the entire equation by 2:
∠ADF+∠BEF=90∘
Step 8: Conclude the proof
Since ∠DFE is the angle formed between the two tangents at point D and point E, we can conclude that:
∠DFE=90∘
Thus, we have proved that ∠DFE=90∘.
---
We have two parallel tangents l and m at points A and B respectively. A tangent at point C intersects the parallel lines at points D and E.
Since l and m are parallel, the angles formed by the tangent at point C with the tangents at points A and B can be analyzed. The angle ∠ADE and ∠BED are formed by the tangent at C with the tangents at points A and B.
By the properties of parallel lines, we know that:
∠ADE+∠BED=180∘
This is because D and E are points on the transversal line CE that intersects the parallel lines l and m.
Now, consider triangles ADF and CDF:
- AD and DC are tangents from point D to the circle, hence AD=DC.
- AF=CF (both are radii of the circle).
- DF=DF (common side).
△ADF≅△CDF
Thus, we have:
∠ADF=∠CDF
Similarly, consider triangles BEF and CEF:
- BE and CE are also tangents from point E to the circle, hence BE=CE.
- BF=CF (both are radii of the circle).
- EF=EF (common side).
△BEF≅△CEF
Thus, we have:
∠BEF=∠CEF
Now, we can express the angles ∠ADE and ∠BED in terms of the angles we found:
∠ADE=∠ADF+∠CDF=2⋅∠ADF
∠BED=∠BEF+∠CEF=2⋅∠BEF
Since we know:
∠ADE+∠BED=180∘
Substituting the expressions we found:
2⋅∠ADF+2⋅∠BEF=180∘
Dividing the entire equation by 2:
∠ADF+∠BEF=90∘
Since ∠DFE is the angle formed between the two tangents at point D and point E, we can conclude that:
∠DFE=90∘
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a circle, PQ and RS are two parallel tangents at A and B. The tangent at makes an intercept DE between PQ and RS. Then ∠DOE is equal to : (where O is centre).
A90∘B120∘C60∘D45∘
XYand X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XYat A and X'Y'at B. Prove that ∠AOB = 90o
View SolutionIn Fig XY and X'Y' are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY and X'Y' at B , prove that ∠AOB=90∘
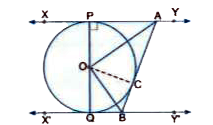
View Solutionlandm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
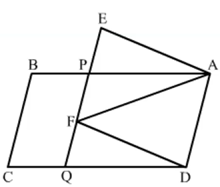
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ
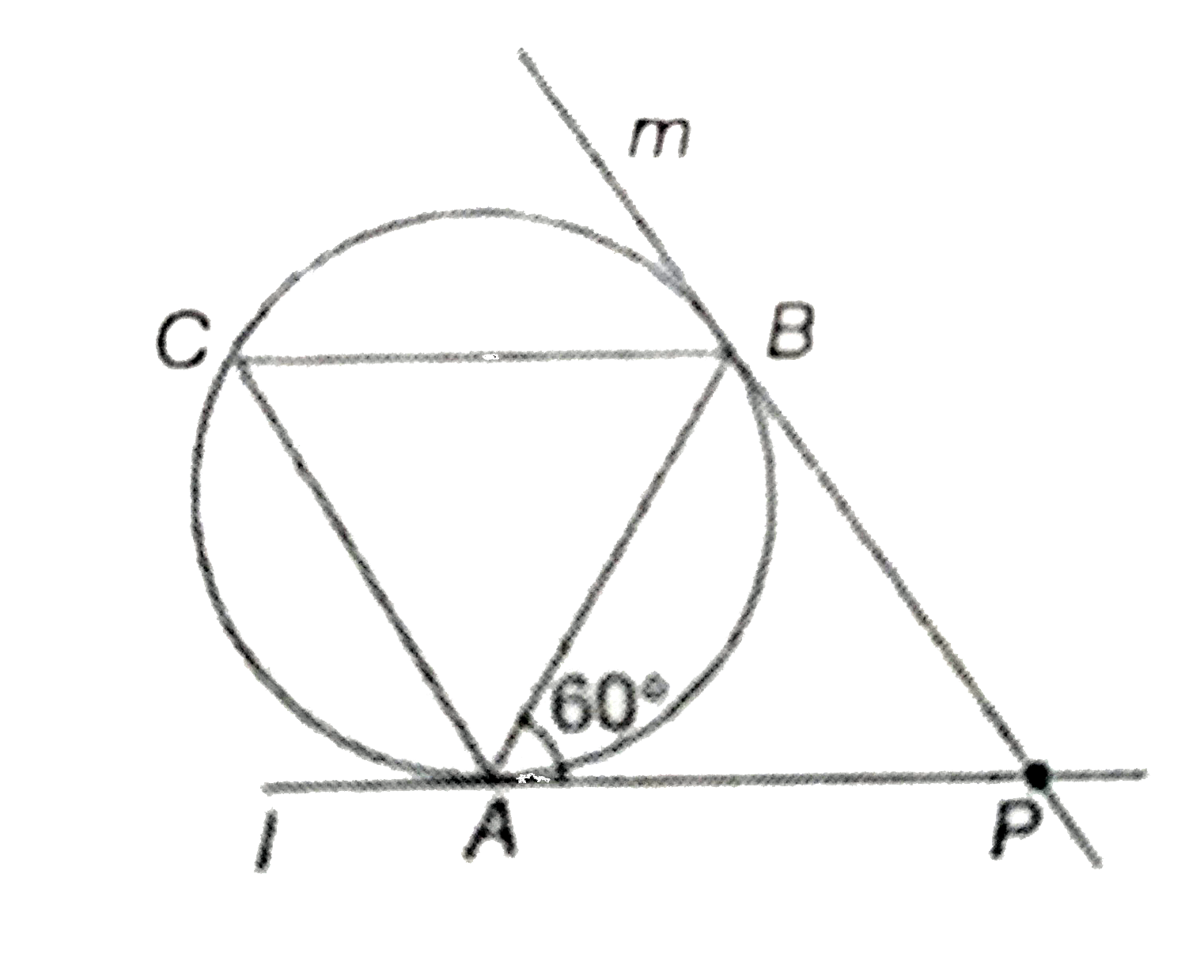
View SolutionIn the following figure, If l and m are two tangents and AB is a chord making and angle of 60∘ with the tangent l, then the angle between l and m is __________.
View SolutionProve that the intercept of a tangent between two parallel tangents to a circle subtends a right angle at the centre.
View SolutionThe common tangents AB and CD to two circles with centres O and O' intersect at E between the centres. Prove that the points O, E and O' are collinear.
View Solution