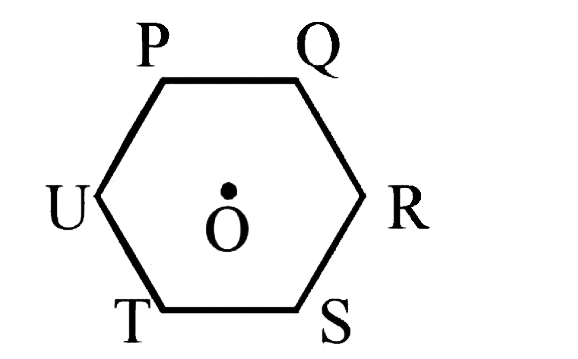
PQRSTU is a regular hexagon. Determine each angle of triangle PQT .
To determine each angle of triangle PQT in the regular hexagon PQRSTU, we can follow these steps:
Step 1: Understand the properties of a regular hexagon
A regular hexagon has all sides equal and all interior angles equal. The formula for the sum of the interior angles of a polygon is given by:
Sum of interior angles=(n−2)×180∘
where n is the number of sides.
Step 2: Calculate the sum of the interior angles of the hexagon
For a hexagon, n=6:
Sum of interior angles=(6−2)×180∘=4×180∘=720∘
Step 3: Calculate each interior angle of the hexagon
Since the hexagon is regular, each interior angle can be calculated by dividing the total sum by the number of angles:
Each angle=720∘6=120∘
Thus, each angle of the hexagon PQRSTU is 120∘.
Step 4: Analyze triangle PQT
In triangle PQT, we know:
- Angle P (which is ∠PQT) is 120∘.
- The triangle PQT is isosceles because PQ=PT (both are sides of the regular hexagon).
Step 5: Use the angle sum property of triangle PQT
The sum of the angles in any triangle is 180∘:
∠P+∠Q+∠T=180∘
Substituting the known value of ∠P:
120∘+∠Q+∠T=180∘
Step 6: Simplify to find angles Q and T
Let ∠Q=∠T (since triangle PQT is isosceles):
120∘+2∠Q=180∘
Subtract 120∘ from both sides:
2∠Q=60∘
Now divide by 2:
∠Q=30∘
Thus, ∠T is also 30∘.
Final Answer
The angles of triangle PQT are:
- ∠P=120∘
- ∠Q=30∘
- ∠T=30∘
A regular hexagon has all sides equal and all interior angles equal. The formula for the sum of the interior angles of a polygon is given by:
Sum of interior angles=(n−2)×180∘
where n is the number of sides.
For a hexagon, n=6:
Sum of interior angles=(6−2)×180∘=4×180∘=720∘
Since the hexagon is regular, each interior angle can be calculated by dividing the total sum by the number of angles:
Each angle=720∘6=120∘
Thus, each angle of the hexagon PQRSTU is 120∘.
In triangle PQT, we know:
- Angle P (which is ∠PQT) is 120∘.
- The triangle PQT is isosceles because PQ=PT (both are sides of the regular hexagon).
The sum of the angles in any triangle is 180∘:
∠P+∠Q+∠T=180∘
Substituting the known value of ∠P:
120∘+∠Q+∠T=180∘
Let ∠Q=∠T (since triangle PQT is isosceles):
120∘+2∠Q=180∘
Subtract 120∘ from both sides:
2∠Q=60∘
Now divide by 2:
∠Q=30∘
Thus, ∠T is also 30∘.
The angles of triangle PQT are:
- ∠P=120∘
- ∠Q=30∘
- ∠T=30∘
Topper's Solved these Questions
Similar Questions
In Figure, PQRS is a square. Determine ∠SRP.
View SolutionIn Figure, PQRS is a square and SRT is an equilateral triangle. Prove that PT=QT (ii) ∠TQR=150
View SolutionA straight line through the vertex P of a triangle PQR intersects the side QR at the points S and the cicumcircle of the triangle PQR at the point T. If S is not the center of the circumcircle, then 1PS+1ST<2√QS×SR 1PS+1ST>2√QS×SR 1PS+1ST<4QR 1PS+1ST>4QR
View SolutionIn ΔPQR,right angled at Q, PR+QR=25cm and PQ=5cm. Determine the values of sinP,cosP and tanP.
View SolutionIn ΔPQR,right angled at Q, PR+QR=25cm and PQ=5cm. Determine the values of sinP,cosP and tanP.
View Solutionsix charges of equal magnitude, 3 poistive and 3 negative are to be placed on PQRSTU corners of a regular hexagon, such that field at the centre is double that of what it would have been if only one +ve charge is placed at R. Which of the following arrangement of charge is posisble for P, Q, R, S, T and U respectively.
View SolutionEach side of triangle ABC is divided into three equal parts. Find the ratio of the area of hexagon PQRSTU to the area of the triangle ABC.
View SolutionLet p,q,r and s represent simple statements. Assume that p is false, q is true, r is false, and s is true. Determine the truth value of each statement expressed below :
q∧r
View SolutionLet p,q,r and s represent simple statements. Assume that p is false, q is true, r is false, and s is true. Determine the truth value of each statement expressed below :
s∧q
View SolutionLet p,q,r and s represent simple statements. Assume that p is false, q is true, r is false, and s is true. Determine the truth value of each statement expressed below :
q∨s
View Solution
