PA and PB are tangents to a circle S touching it at points A and B. C is a point on S in between A and B as shown in the figure. LCM is a tangent to S intersecting PA and PB in S at points L and M, respectively. Then the perimeter of the triangle PLM depends on o
A,B,C and P
P but not on C
P and C only
the radius of S only
The correct Answer is:B
To solve the problem, we need to find the perimeter of triangle PLM, where PA and PB are tangents to the circle S, and LCM is another tangent intersecting PA and PB at points L and M.
1. Understanding the Geometry:
- PA and PB are tangents to the circle S at points A and B, respectively.
- C is a point on the circle S between A and B.
- LCM is a tangent to the circle S intersecting PA at L and PB at M.
2. Identifying the Segments:
- The lengths of the tangents from a point outside the circle to the points of tangency are equal. Thus, we have:
- PL=PA (since L is on PA)
- PM=PB (since M is on PB)
3. Using the Tangent Properties:
- Since LCM is a tangent to the circle, we can also say:
- PL+LC=LA (because LA is the entire tangent from P to A)
- CM+PM=BM (because BM is the entire tangent from P to B)
4. Finding the Perimeter:
- The perimeter of triangle PLM can be expressed as:
Perimeter=PL+LM+PM
- From our earlier observations:
- PL=PA
- PM=PB
- Therefore, we can express LM in terms of the tangents:
LM=LC+CM
- Substituting the values:
Perimeter=PA+PB+(LC+CM)
- Since LC+CM can be expressed in terms of the tangents to the circle, we can simplify this further.
5. Final Expression:
- The perimeter of triangle PLM can be simplified to:
Perimeter=PA+PB+(LA+BM)
- Since LA=PA and BM=PB, we can conclude:
Perimeter=PA+PB+PA+PB=2(PA+PB)
Conclusion:
Thus, the perimeter of triangle PLM depends on the lengths of the tangents PA and PB.
- PA and PB are tangents to the circle S at points A and B, respectively.
- C is a point on the circle S between A and B.
- LCM is a tangent to the circle S intersecting PA at L and PB at M.
- The lengths of the tangents from a point outside the circle to the points of tangency are equal. Thus, we have:
- PL=PA (since L is on PA)
- PM=PB (since M is on PB)
- Since LCM is a tangent to the circle, we can also say:
- PL+LC=LA (because LA is the entire tangent from P to A)
- CM+PM=BM (because BM is the entire tangent from P to B)
- The perimeter of triangle PLM can be expressed as:
Perimeter=PL+LM+PM
- From our earlier observations:
- PL=PA
- PM=PB
- Therefore, we can express LM in terms of the tangents:
LM=LC+CM
- Substituting the values:
Perimeter=PA+PB+(LC+CM)
- Since LC+CM can be expressed in terms of the tangents to the circle, we can simplify this further.
- The perimeter of triangle PLM can be simplified to:
Perimeter=PA+PB+(LA+BM)
- Since LA=PA and BM=PB, we can conclude:
Perimeter=PA+PB+PA+PB=2(PA+PB)
Thus, the perimeter of triangle PLM depends on the lengths of the tangents PA and PB.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Multiple Correct Answers Type
9 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - MATRIX MATCH TYPE
7 Videos
- COMPLEX NUMBERSBOOK - CENGAGE ENGLISHCHAPTER - COMPLEX NUMBERSEXERCISE - MATRIX MATCH TYPE
9 Videos
Similar Questions
From an external point P, tangents PA and PB are drawn to a circle. CE is a tangent to the circle at D which intersect PA and PB at point E and C respectvely. If AP=15 cm, find the permeter of the △PEC.
View SolutionFrom an external point P, two tangents, PA and PB are drawn to a circle with centre 0. At one point E on the circle tangent is drawn which intersects PA and PB at C and D, respectively. If PA=10 cm, find the perimeter of the triangle PCD.
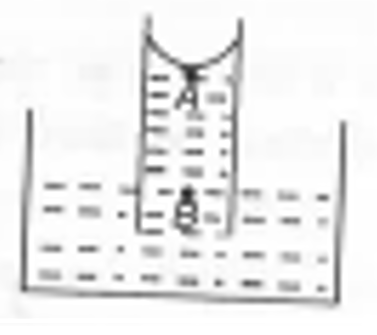
View SolutionA capillary tube is dipped in water as shown in the figure. If P0 is the atmospheric pressure, PA and PB are pressure at A and B respectively then
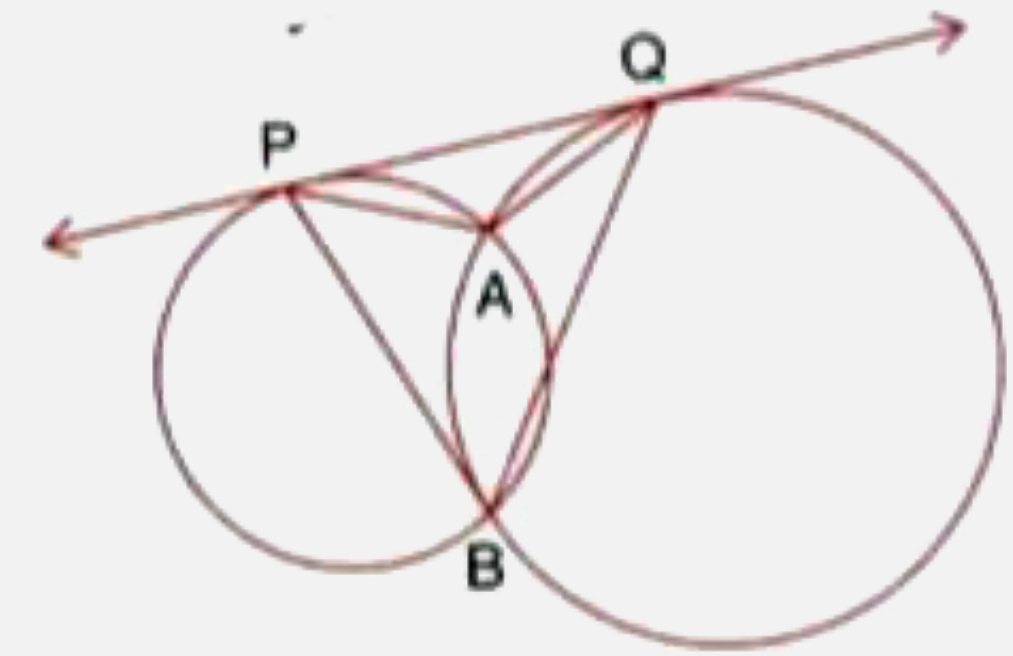
View SolutionTwo circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
View SolutionPAandPB are tangents from P to the circle with centre O. At point M, a tangent is drawn cutting PA at K and PB at N. Prove that KN=AK+BN.
View Solutionlandm are two parallel tangents to a circle with centre O, touching the circle at A and B respectively. Another tangent at C intersects the line l at D and m at E. Prove that∠DOE=90∘.
View SolutionFrom an external point P , tangents PA and PB drawn to a circle with centre O . If CD is the tangent to the circle at a point E and PA=14cm , find the perimeter of PCD .
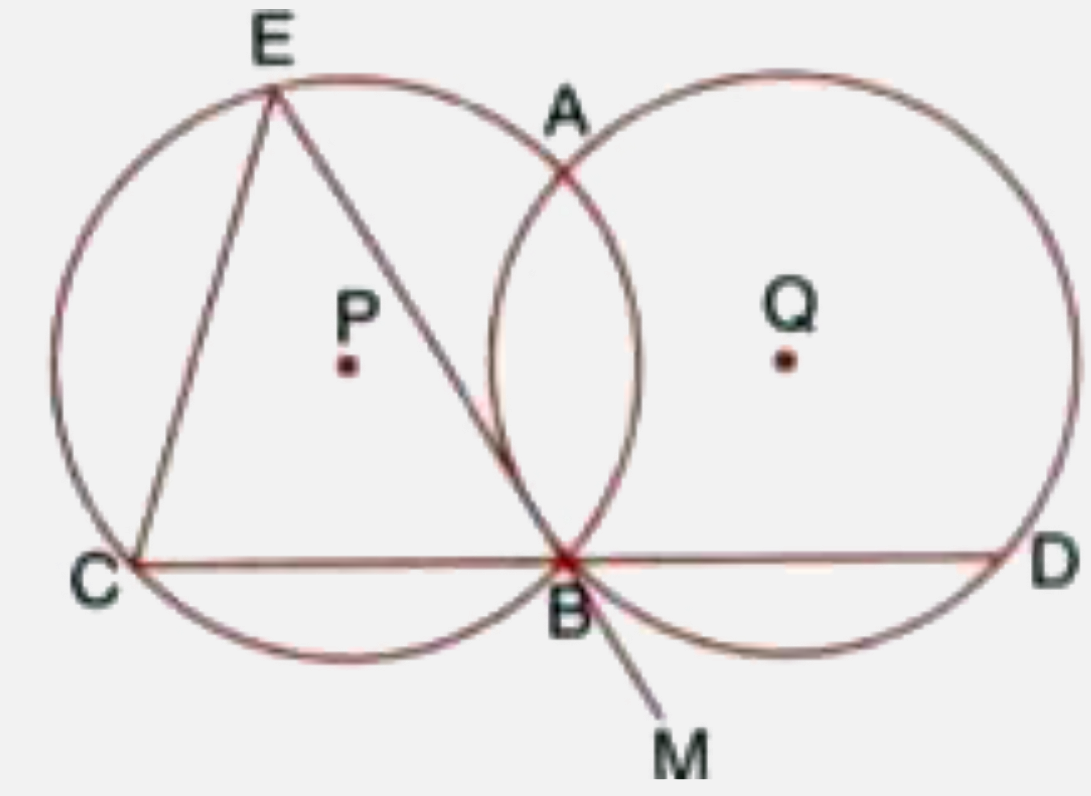
View SolutionCircles with centres P and Q intersects at points A and B as shown in the figure. CBD is a line segment and EBM is tangent to the circle, with centre Q, at point B. If the circles are congruent, show that : CE = BD.
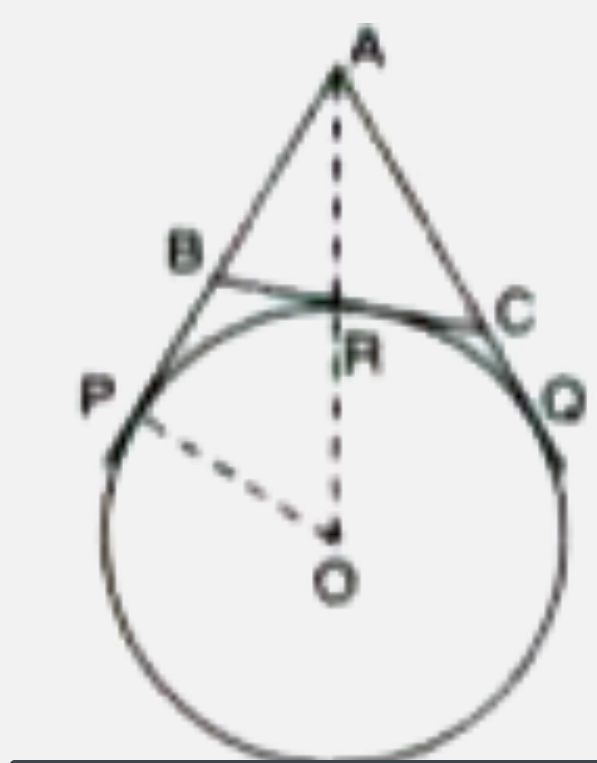
View SolutionIn the given figure AP and AQ are tangents to the circle with centre O. BC is tangent at point R on it.
If OA=17 cm and radius of the circle =8cm, find the perimeter of the triangle ABC.
View SolutionIf A and B are two fixed points and P is a variable point such that PA+PB=4, the locus of P is
View Solution
