Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary.
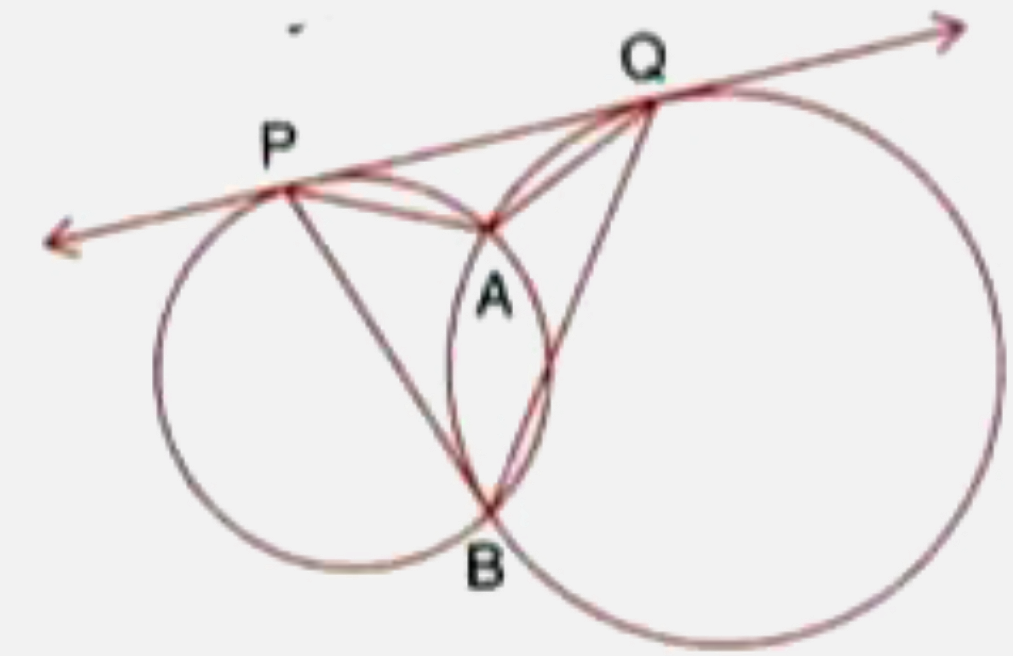
Step by step video & image solution for Two circles intersect each other at point A and B. Their common tangent touches the circles at points P and Q as shown in the figure. Show that the angles PAQ and PBQ are supplementary. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (C)
42 Videos
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18(A)
24 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
Two circles intersect each other at points A and B. A straight line PAQ cuts the circles at P and Q. If the tangents at P and Q intersect at point T, show that the points P, B, Q and T are concylic.
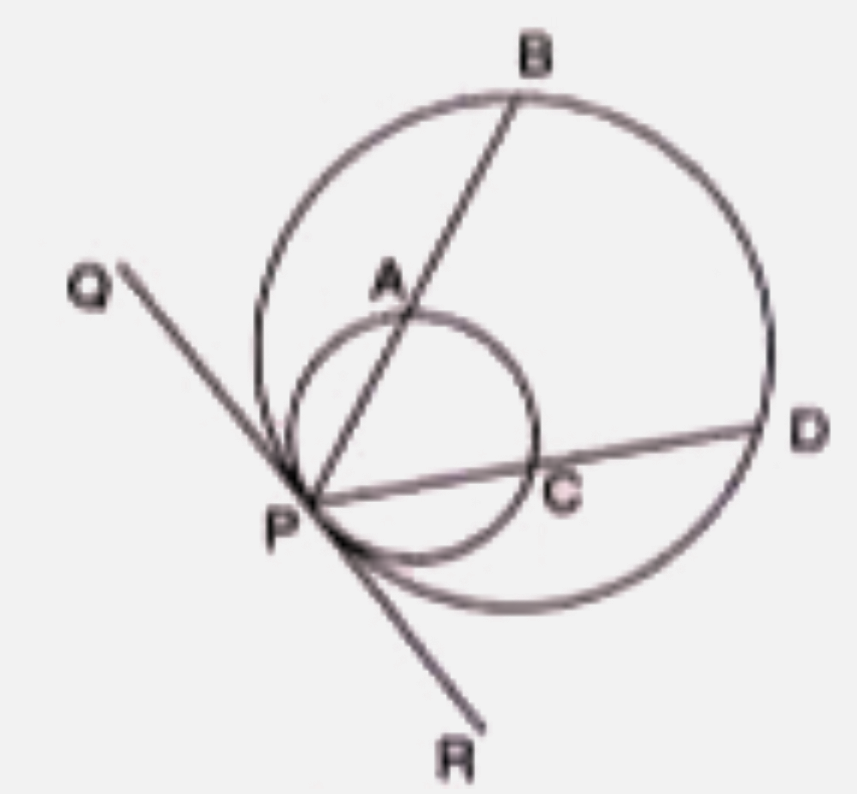
View SolutionTwo circles touch each other internally at point P. QPR is the tangent at P, segments PAB and PCD meet circles at points, A,B,C and D as shown in the figure.
Show that chord AC is parallel to chord BD.
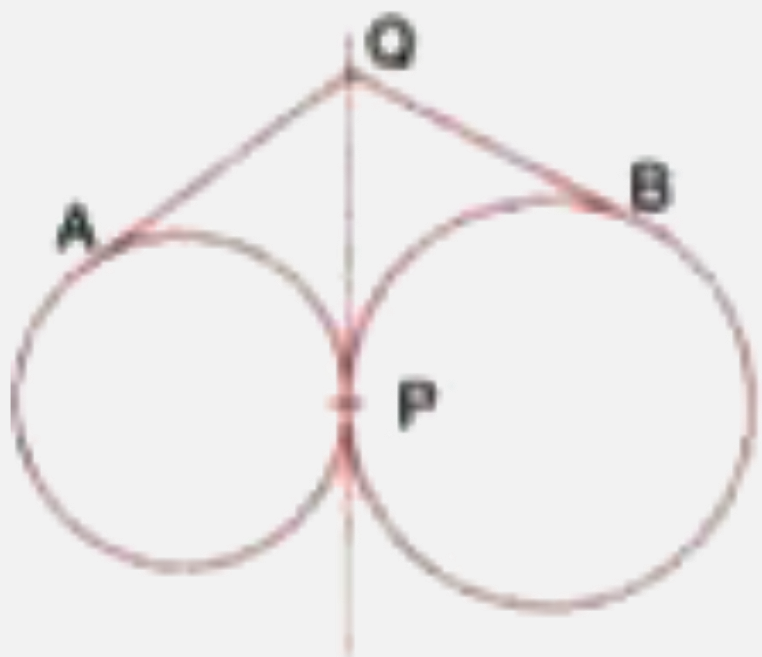
View SolutionTwo congruent circles intersect each other at points A and B. Through A any linesegment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
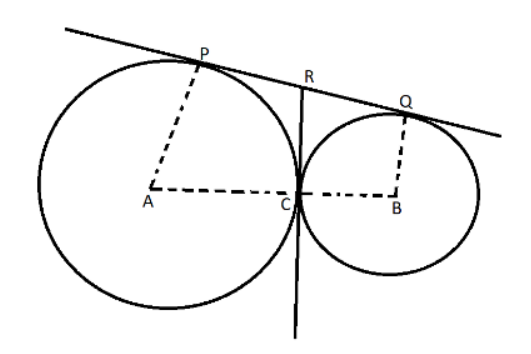
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circels. Prove that PBQ is a straight line.

View SolutionIn the figure, two circles intersect each other at points A and B. AP and AQ are the diameters of these circels. Prove that PBQ is a straight line.

View SolutionLet P and Q be 2 circles externally touhing each other at point X. Line segment AB is a direct common tangent to circle P and Q at points A and B respectively. Another common tangent to P and Q at X intersects line AB at a point Y. If BY = 10 units and the radius of P is 9 units, then the value of the reciprocal of the radius of the radius of the circle Q is equal to
View SolutionTwo equal circles touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB= 60o (b) 45o (c) 30o (d) 90o
View Solution
