Plot the region in the first quadrant in which points are nearer to the origin than to the line x=3.Solution in Bengali
Point P(x,y) lies in the first quadrant. Therefore, x,y>0
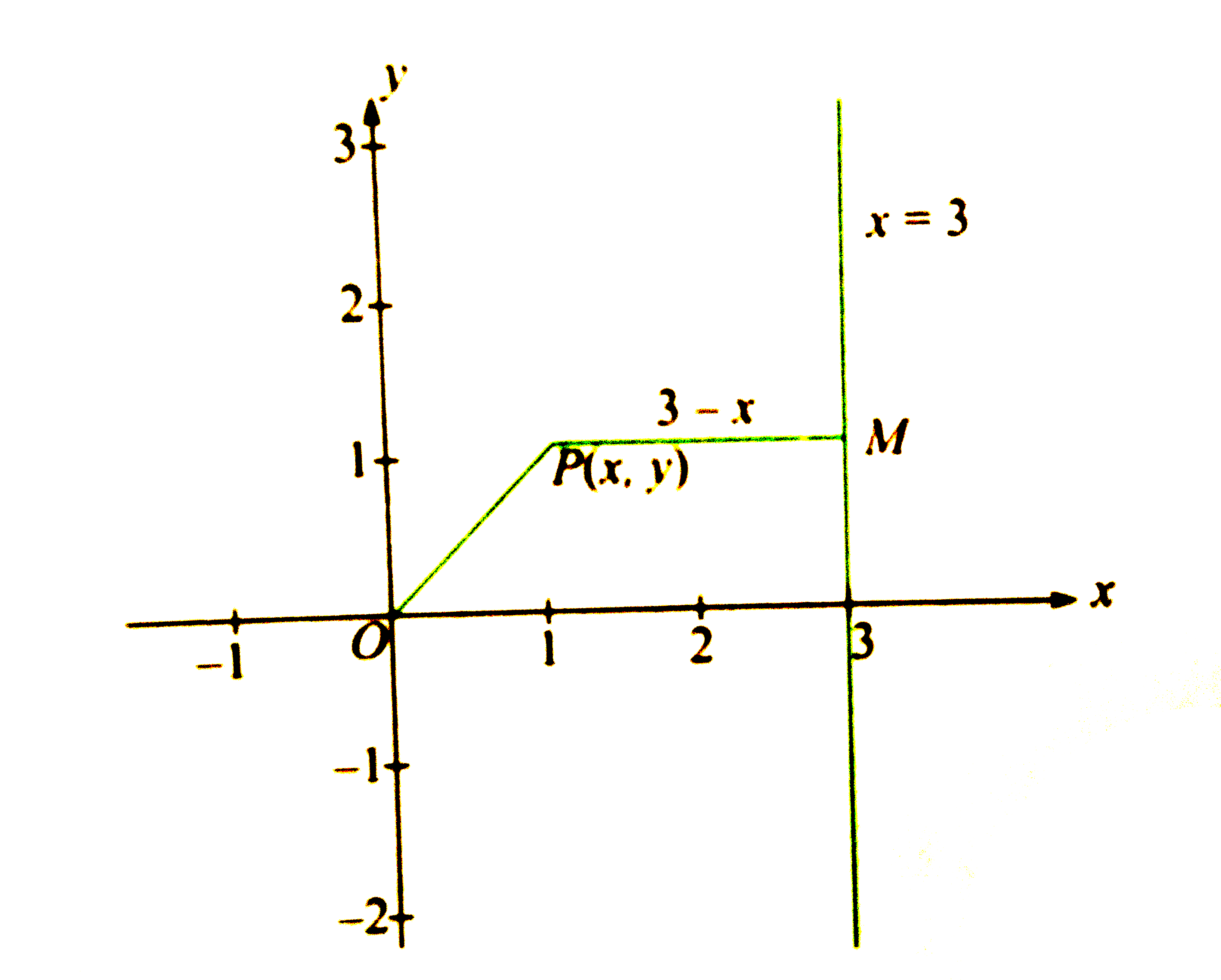
Also point P(x,y) is nearer to the origin than to the line x=3
Now OP=√x2+y2
Distance of P from line x-3=0 is PM =3-x
According to the question, OP<PM
⇒ √x2+y2<(3−x)
or x2+y2<x2−6x+9
or y2<−6x+9
or y2<−6(x−32)
Points satisfying above inequality lie inside parabola y2=9−6x in the first quadrant.
Parabola y2=−6(x−32) is concave to the left, having axis as
x-axis and vertex at (32,0) and directrix x=3
The required region as shown in the figure.

Area of the region =3∫09−y26dy=16(9y−y33)30
=16(27−9)=3 sq. units
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Solved Examples
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Concept Application Exercise 9.1
9 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
Find the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionFind the area of the smaller part of the circle x2+y2=a2 cut off by the line x=a√2.
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.
View SolutionThe point (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
View SolutionFind the area of the region if the first quadrant bounded by the parabola y2=4x, the line x+y=3 and y-axis.
View SolutionThe points (other than origin) for which abscissa is equal to the ordinate will lie in the quadrant
View SolutionArea of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle x2+y2=32 is
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
View SolutionPlot the region in the first quadrant in which points are nearer to the origin than to the line x=3.
View SolutionConsider two regions
R1:points P are nearer to (1,0) than to x=−1.
R2:Points P are nearer to (0,0) than to (8,0) Find the area of the region common to R1andR2.
View SolutionThe area of the region bounded by the curve y2=xand the Y axis in the first quadrant and lines y=3andy=9 is ______
View Solution