Point A lies on curve y=e−x2 and has the coordinates (x,e−x2) where x>0 Point B has coordinates (x,o) If 'O' is the origin, then the maximum area of ΔAOB is :
1√8e
1√4e
1√2e
1√e
The correct Answer is:A
Step by step video solution for Point A lies on curve y = e^(-x ^(2)) and has the coordinates (x, e ^(-x ^(2))) where x gt 0 Point B has coordinates (x,o) If 'O' is the origin, then the maximum area of Delta AOB is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VK JAISWAL ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - EXERCISE (ONE OR MORE THAN ONE ANSWER IS/ARE CORRECT)4videos
AREA UNDER CURVES
- BOOK - VK JAISWAL ENGLISHCHAPTER - AREA UNDER CURVESEXERCISE - EXERCISE (COMPREHENSION TYPE PROBLEMS)6videos
AREA UNDER CURVES
- BOOK - VK JAISWAL ENGLISHCHAPTER - APPLICATION OF DERIVATIVES EXERCISE - EXERCISE (SUBJECTIVE TYPE PROBLEMS)22videos
APPLICATION OF DERIVATIVES
- BOOK - VK JAISWAL ENGLISHCHAPTER - BIONMIAL THEOREMEXERCISE - Exercise-4 : Subjective Type Problems16videos
BIONMIAL THEOREM
Similar Questions
Point A lies on the curve y=ex2 and has the coordinate (x,e−x2) where x>0. Point B has the coordinates (x,0). If 'O' is the origin, then the maximum area of the ΔAOB is
View SolutionPoint O has coordinates (0, 0), point P lies on the graph of y=6−x2, and point B has coordinates (2√3,0). If OP=BP, the area of triangle OPB is
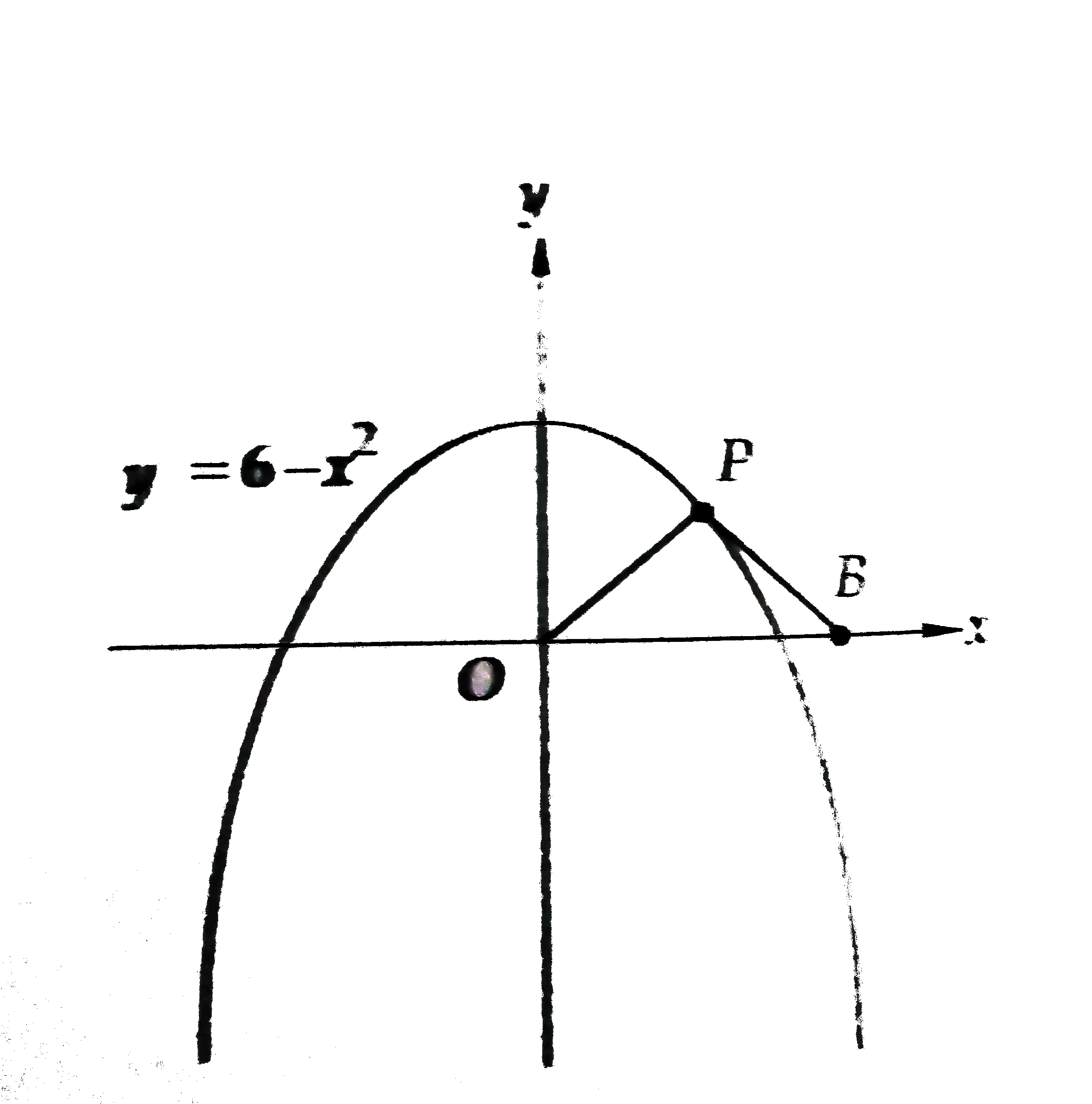 View Solution
View SolutionThe area enclosed between the curve y=loge(x+e) and the coordinate axes is
View SolutionThe coordinates of the image of the origin O with respect to the line x+y+1=0 are
View SolutionIf the length of sub-normal is equal to the length of sub-tangent at any point (3,4) on the curve y=f(x) and the tangent at (3,4) to y=f(x) meets the coordinate axes at AandB , then the maximum area of the triangle OAB, where O is origin, is 45/2 (b) 49/2 (c) 25/2 (d) 81/2
View SolutionIf the length of sub-normal is equal to the length of sub-tangent at any point (3,4) on the curve y=f(x) and the tangent at (3,4) to y=f(x) meets the coordinate axes at AandB , then the maximum area of the triangle OAB, where O is origin, is 45/2 (b) 49/2 (c) 25/2 (d) 81/2
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionFind the points on the curve y=x3 where the slope of the tangent is equal to x-coordinate of the point.
View SolutionFor the curve y=xex , the point
View SolutionThe coordinates of the point P are (−3, 2) . Find the coordinates of the point Q which lies on the line joining P and origin such that OP=OQ .
View Solution

