Point O has coordinates (0, 0), point P lies on the graph of y=6−x2, and point B has coordinates (2√3,0). If OP=BP, the area of triangle OPB is
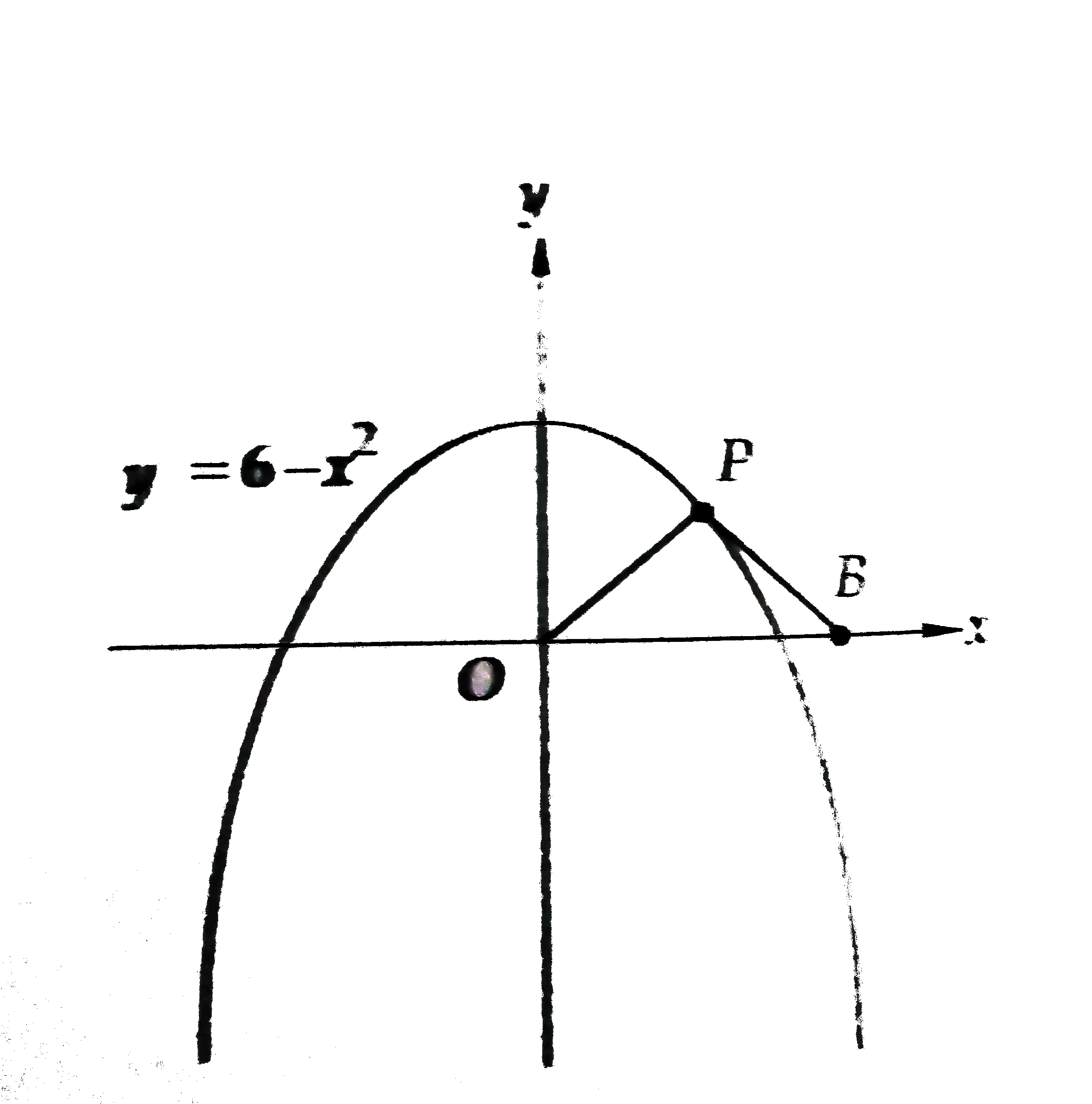
1.7
3.0
3.5
5.2
The correct Answer is:D
To find the area of the triangle, you want the base and the height. The base is the length OB, which is simply the x - coordinate of point B:2√3. The height is the y - coordinate of point P, which is equal to 6−x2. The triangle is isosceles, so the altitude from P to base OB divides the base in hald and the x - coordinate for point P is √3. Plug x=√3 into the equation y=6−x2 to find the height :
height =6−(√3)2=6−3=3
So if the base is 2√3 and the height is 3 :
Area =12 (base) (height)
=12(2√3)(3)=3√3≈5.2
Topper's Solved these Questions
Similar Questions
Knowledge Check
Line segment ¯¯¯¯¯¯AB has midpoint (7,-1) . If point A has coordinates (2,6) , then point B has coordinates
A(92,52)B(192,−92)C(12,-8)D(14,-8)A point R with x - coordinate 4 lies on the line segment joining the points P(2,-3,4) and Q(8, 0, 10) . The coordinates of R are
A(4, -2, 6)B(-4,-2,6)C(-4,2,6)D(4,2,6)
In the ΔABC, the coordinates of B are (0,0),AB=2,∠ABC=π3 and the middle point of BC has the coordinates (2,0). The centroid of the triangle is
View Solutionif P,Q are two points on the line 3x+4y+15=0 such that OP=OQ=9 then the area of triangle OPQ is
View SolutionIn the xy-coordinate plane, the graph of y=5x2−12x intersects the grphs of y=−2 at points (0,0) and (a,b). What is the value of a ?
View SolutionThe equation of the base of an equilateral triangle is x+y−2=0 and the opposite vertex has coordinates (2, -1). Find the area of the triangle.
View SolutionPoint A lies on the curve y=ex2 and has the coordinate (x,e−x2) where x>0. Point B has the coordinates (x,0). If 'O' is the origin, then the maximum area of the ΔAOB is
View SolutionA point with z-coordinate 6 lies on the line segment joining the points (2, 1, 2) and (6, 0, 8).
Find the coordinates of the point.
View Solution