Point P (2,-7) is the centre of a circle with radius 13 units, PT is perpendicular to chord AB and T= (-2,-4). Calculate the length
AT
The correct Answer is:5 units
To solve the problem step by step, we will follow these instructions:
Step 1: Identify the Given Information
- Center of the circle, P(2,−7)
- Radius of the circle, r=13 units
- Point T(−2,−4) where PT is perpendicular to chord AB
Step 2: Calculate the Length of PT
We will use the distance formula to find the length of PT. The distance formula between two points (x1,y1) and (x2,y2) is given by:
d=√(x2−x1)2+(y2−y1)2
Substituting the coordinates of points P(2,−7) and T(−2,−4):
PT=√((−2)−2)2+((−4)−(−7))2
PT=√(−4)2+(3)2
PT=√16+9
PT=√25=5
Step 3: Use the Pythagorean Theorem in Triangle APT
Since PT is perpendicular to chord AB, triangle APT is a right triangle. We can apply the Pythagorean theorem:
AP2=PT2+AT2
Where:
- AP is the radius of the circle, which is 13 units.
- PT is calculated as 5 units.
- AT is the length we want to find.
Substituting the known values:
132=52+AT2
169=25+AT2
AT2=169−25
AT2=144
Step 4: Calculate AT
Taking the square root of both sides:
AT=√144=12
Final Answer
The length of AT is 12 units.
---
- Center of the circle, P(2,−7)
- Radius of the circle, r=13 units
- Point T(−2,−4) where PT is perpendicular to chord AB
We will use the distance formula to find the length of PT. The distance formula between two points (x1,y1) and (x2,y2) is given by:
PT=√(−4)2+(3)2
PT=√16+9
PT=√25=5
Since PT is perpendicular to chord AB, triangle APT is a right triangle. We can apply the Pythagorean theorem:
- AP is the radius of the circle, which is 13 units.
- PT is calculated as 5 units.
- AT is the length we want to find.
169=25+AT2
AT2=169−25
AT2=144
Taking the square root of both sides:
The length of AT is 12 units.
Similar Questions
Points P (2, 7) is the centre of a circle with radius 13 unit, PT is perpendicular to chord AB and T = (-2, -4), Calculate the length of ,

(i) AT
(ii) AB.
View SolutionO is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
View Solution
Knowledge Check
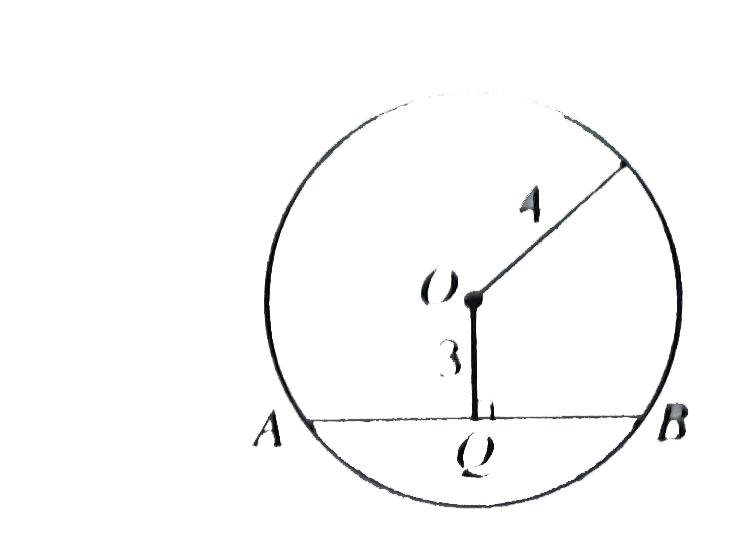
A chord ¯¯¯¯¯¯AB is 3 cm. from the center of a circle with radius 4. What is the length of chord ¯¯¯¯¯¯AB ?A√7B2√7C5D10
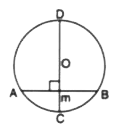
In the given figure, the diameter CD of a circle with centre 0 is perpendicular to the chord AB.
If AB = 8 cm and CM = 2 cm, find the radius of the circle.
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionThe points P (-2,4) lies on a circle of radius 6 and centre (3,5).
View SolutionThe radius of a circle is 17-0 cm and the length of perpendicular drawn from its centre to a chord is 8 0 cm. Calculate the length of the chord.
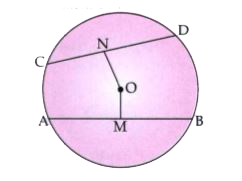
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
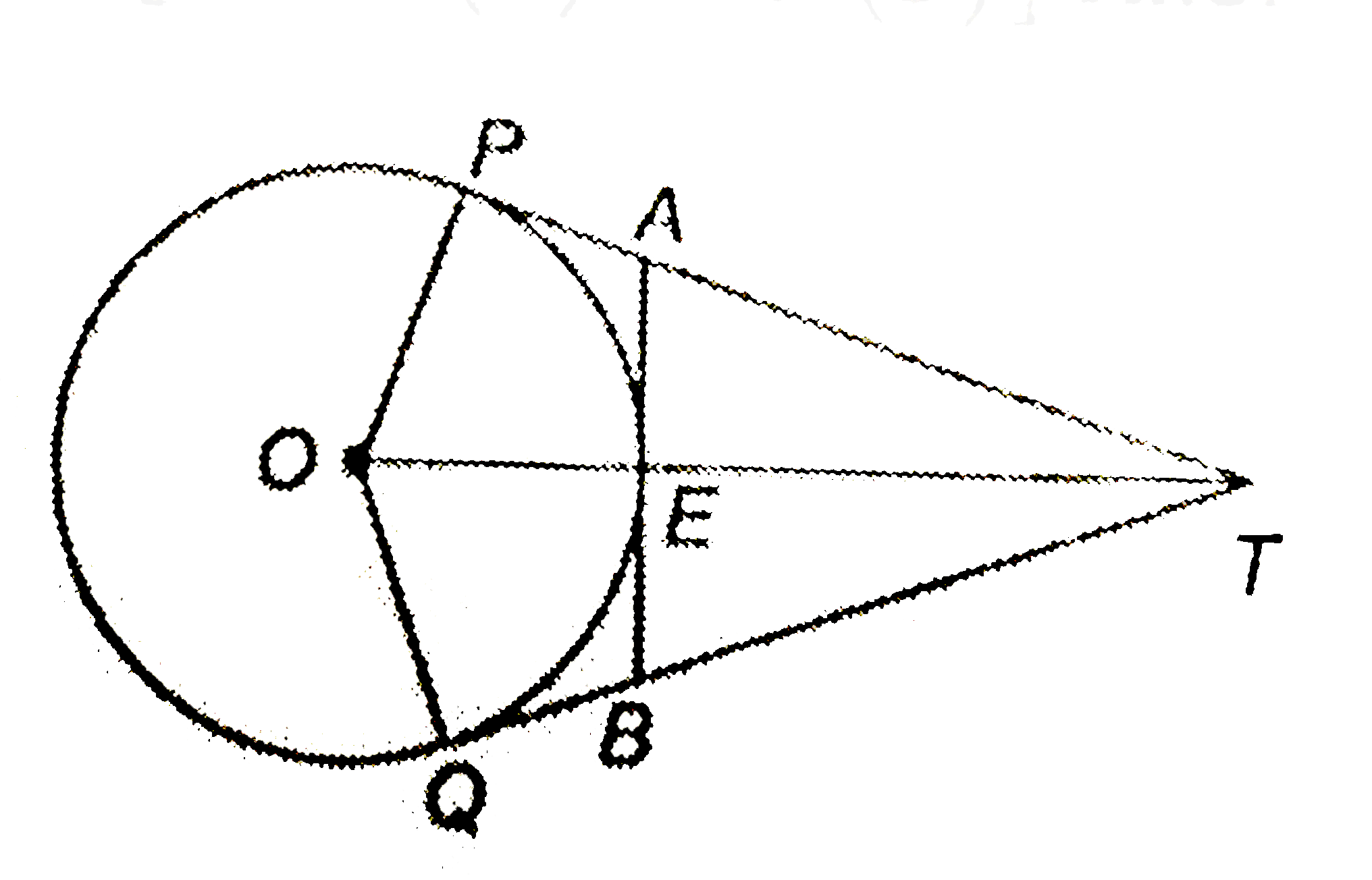
View SolutionAs shown in the given figure, from an external point P, a tangent PT and a line segment PAB are drawn to a circle with centre O. ON is perpendicular on the chord AB, Prove that
PA.PB=PN2−AN2
View SolutionA point "P" is at the 9 unit distance from the centre of a circle of radius 15 units. The total number of different chords of the circle passing through point P and have integral length is
View Solution
