Points X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS The line XY cuts the line PR at Z Find the ratio PZ: ZR
2125−−→PR
1625−−→PR
1725−−→PR
None of these
The correct Answer is:A
4(5→a+→b)5+→a+5→b5=21(→a+→b)25=2125−−→PR

P.V. of X is 4(→a+→b)5=5→a+4→b5
P.V.of Y is 4→b+→a+→b5=→a+5→b5
Now, −−→PZ=m−−→PR
−−→PZ=m(→a+→b)
Let Z divides YX in the ratio λ:1
P.V. of Z=λ−−→OX+−−→OYλ+1
∴(−−→PZ)=λ(5→a+→b)5+→a+5→b5λ+1=m(→a+→b)
Comparing coefficients of →a and →b
m=5λ+15(λ+1) and m=4λ+55(λ+1)
∴λ=4
∴λ(PZ)=4(5→a+4→b)5+→a+5→b54+1
=21(→a+→b)25=2125−−→PR
Topper's Solved these Questions
Similar Questions
In the adjoining figure, S and T are points on the sides PQ and PR respectively of ΔPQR such that PT=2cm,TR=4cmandST is parallel to QR. Find the ratio of the ares ofΔPSTandΔPQR.
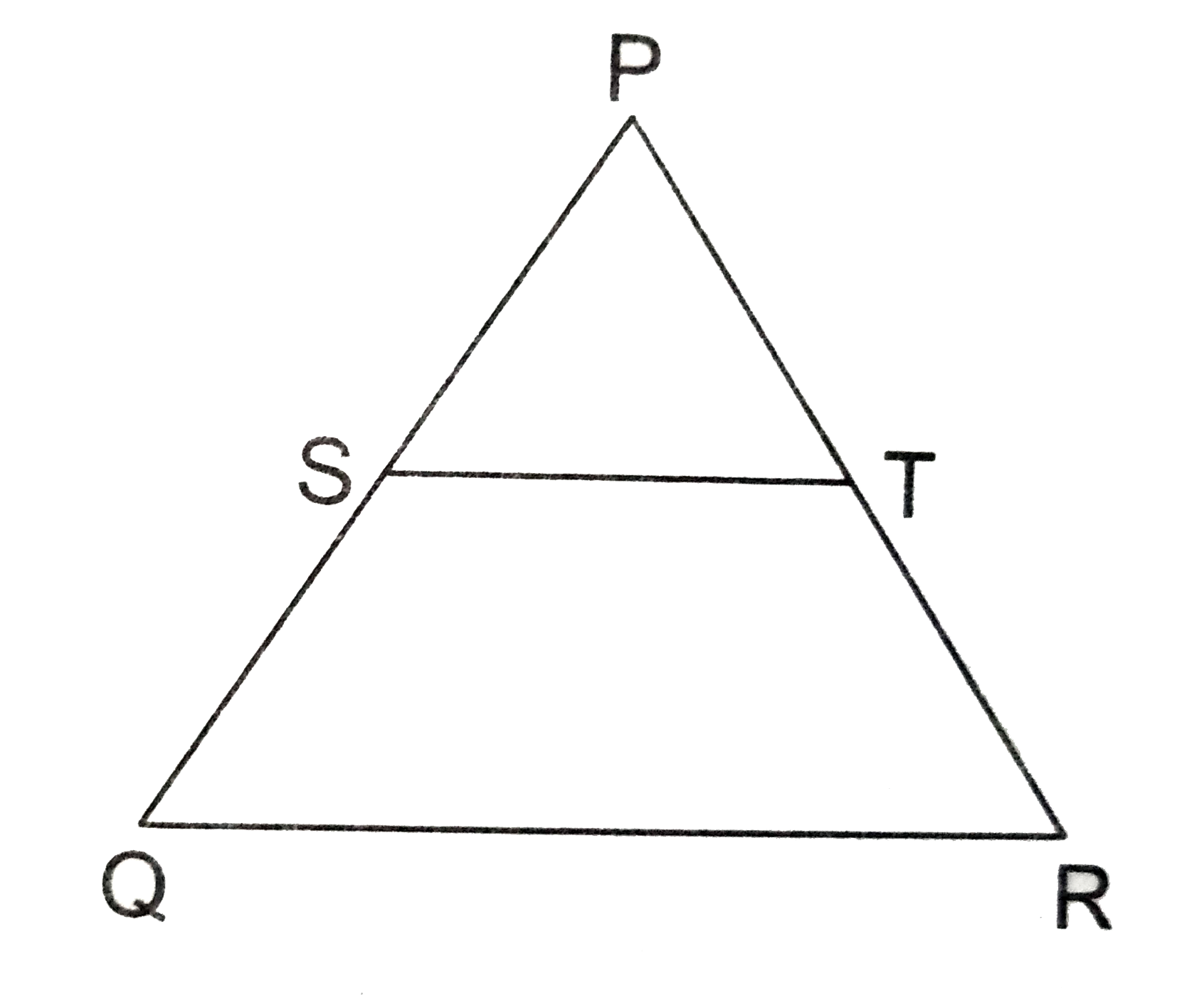
View SolutionS and T are points on the sides PQ and PR, respectively of ΔPQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ΔPST and ΔPQR.
View Solution
Knowledge Check
Points X and Y are taken on the sides QR and RS, respectively of a parallelogram PQRS, so that QX=4XR and RY=4YS. The line XY cuts the line PR at Z. Then, PZ is
A2125PRB1625PRC1725PRDnone of theseThe diagonals of a parallelogram PQRS are along the lines x+3y=4 and 6x-2y=7. Then PQRS must be a
ARectangleBSquareCCyclic QuadrilateralDRhombusThe diagonals of parallelogram PQRS are along the lines x+3y=4 and 6x−2y=7. Then PQRS must be a
ArectangleBsquareCcyclic quadrilateralDrhombus
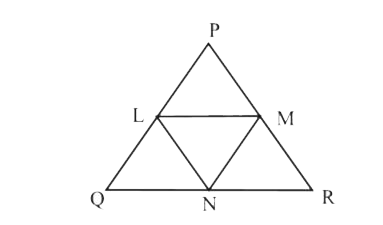
In the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
View SolutionThe diagonals of a parallelogram PQRS are along the lines x+3y =4 and 6x-2y = 7, Then PQRS must be :
View SolutionIn a triangle PQR, S and T are points on QR and PR respectively, such that QS=3SR and PT=4TR. Let M be the point of intersection of PS and QT. Determine the ratio QM:MT
View SolutionIn a triangle PQR,SandT are points on QRandPR, respectively, such that QS=3SRandPT=4TR. Let M be the point of intersection of PSandQT. Determine the ratio QM:MT using the vector method .
View SolutionIn ΔPQR,right-angled at Q,X,Y and Z are points on sides PR,RQandPQrespectively such that QX⊥PR,XY⊥RQandXZ⊥PQ . Find the value of XZ If PZ=4cmandZQ=9cm.
View Solution
