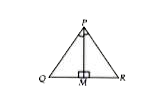
PQR is a triangle in which PM is the bisector of ∠PandPM⊥QR. Prove that:
ΔPMQ≅ΔPMR
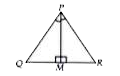
Step by step video & image solution for PQR is a triangle in which PM is the bisector of anglePandPMbotQR. Prove that: DeltaPMQ~=DeltaPMR by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Subjective Problems (Long Answer Type)
10 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Olympiad/HOTS Corner
10 Videos
- CONGRUENCE OF TRIANGLES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - CONGRUENCE OF TRIANGLES EXERCISE - Subjective Problems (Very Short Answer Type)
10 Videos
- COMPARING QUANTITIES BOOK - MTG IIT JEE FOUNDATIONCHAPTER - COMPARING QUANTITIES EXERCISE - Olympaid/HOTS Corner
20 Videos
- DATA HANDLINGBOOK - MTG IIT JEE FOUNDATIONCHAPTER - DATA HANDLINGEXERCISE - Olympiad / Hots Corner
20 Videos
Similar Questions
Knowledge Check
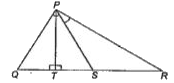
In Δ PQR,PS is the bisector of ∠PandPT⊥QR, where ∠ Q = 60 and ∠R = 30 then ∠TPS is equal to
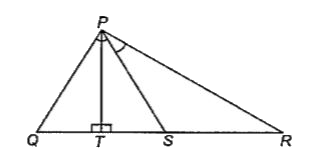 A10B30C60D15
A10B30C60D15In ΔPQR, Ps is the bisector of <P and PT⊥QR, then <TPS is equal to
 A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R)
A<Q+<RB90∘+12<QC90∘−12<RD12(<Q−<R)
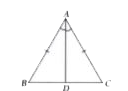
In the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:

BD = CD
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
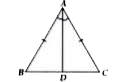
AD⊥BC
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC and AD is the bisector of ∠A. Prove that:
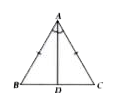
∠B=∠C
View SolutionIn the figure , PS is the bisector of ∠QPR of ΔPQR . Prove that QSSR=PQPR .

View SolutionIn the given figure, PQR is a equilateral triangle and PS is the angle bisector of ∠P. What is the value of RT: RQ ?
View SolutionABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View Solution