PQRS and PABC are two parallelograms of equal area. Prove that QC∣∣BRSolution in Punjabi
Step by step video & image solution for PQRS and PABC are two parallelograms of equal area. Prove that QC||BR by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In the figure. Show that ABCD is a parallelogram.
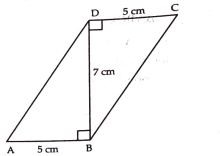 Calculate the area of ||gm ABCD.
Calculate the area of ||gm ABCD.
View SolutionThe radius of a circle is 8 cm and the length of its chords is 12 cm. Fid the distance of the from the centre.
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
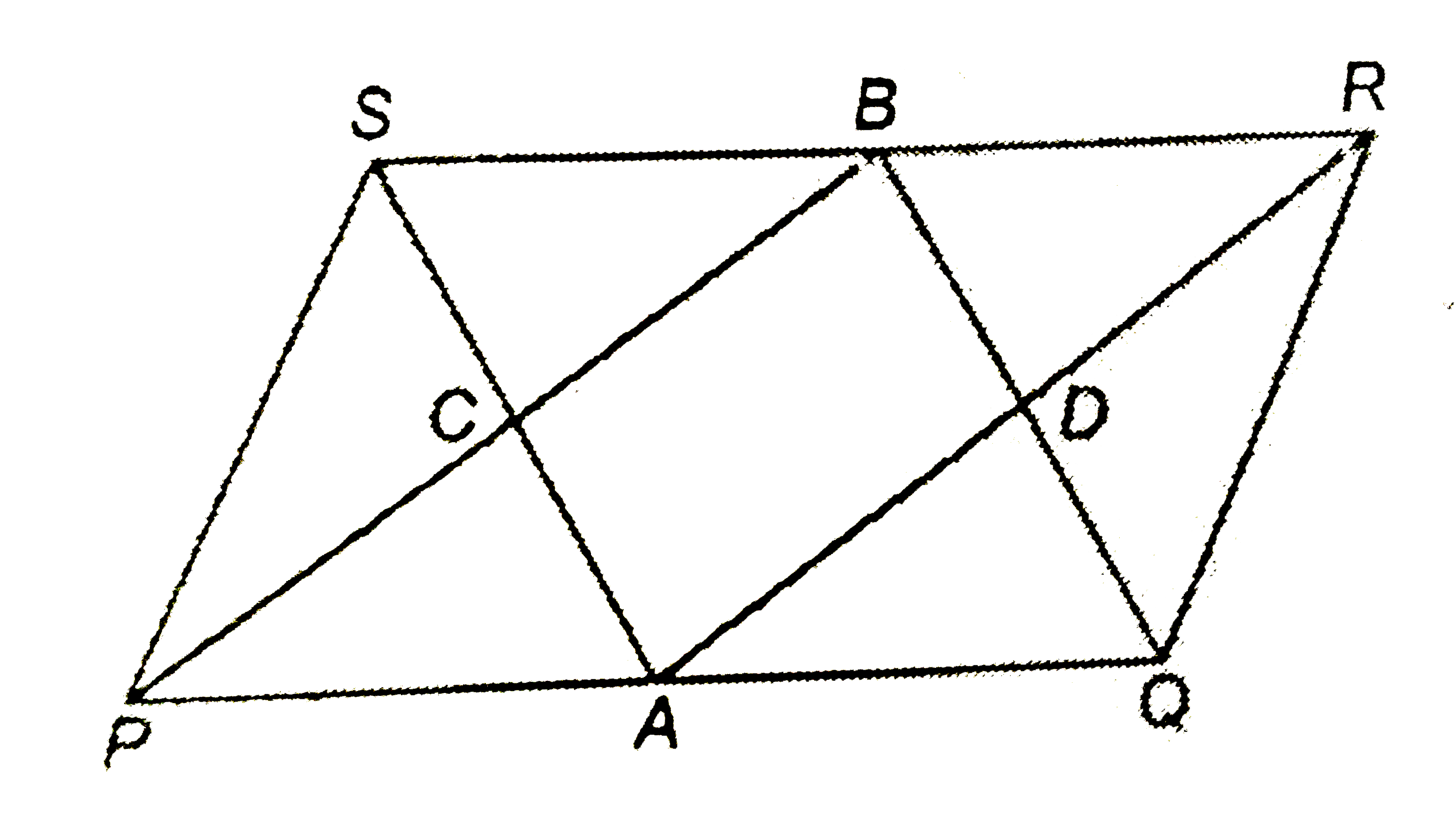
View SolutionIn the adjoining figure, PQRS and PABC are two parallelogram of equal area. Prove that QC||BR.
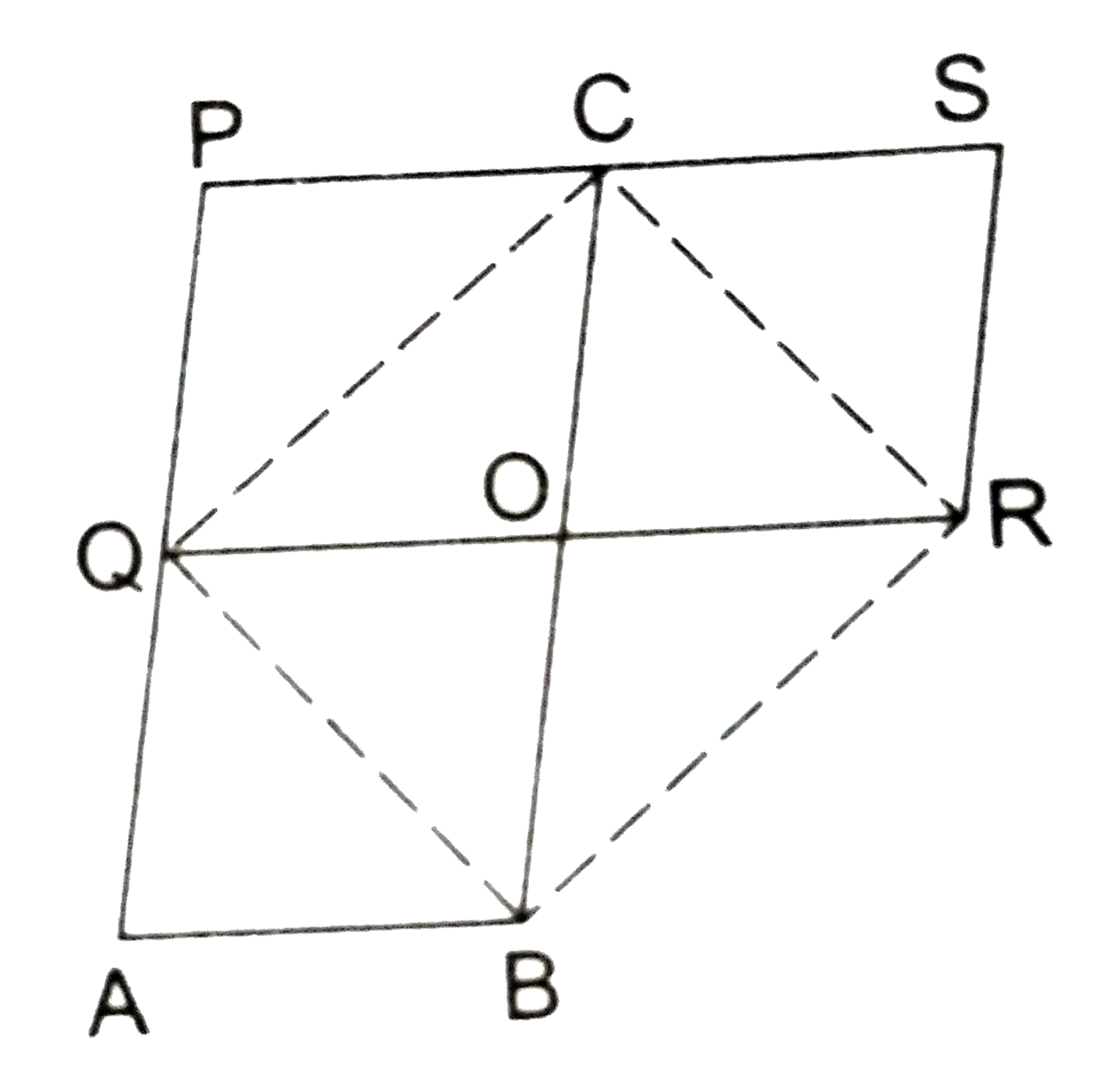
View Solutionसिद्ध कीजिए कि समान्तर चतुर्भुज की सम्मुख भुजाओ के मध्य बिन्दुओं को जोड़ने वाला रेखाखण्ड समान्तर चतुर्भुज को बराबर क्षेत्रफल वाले दो समान्तर चतुर्भुजों में बांटती है।
View Solutionसिद्ध कीजिए कि समान्तर चतुर्भुज के विकर्ण उस समान्तर चतुर्भुज को बराबर क्षेत्रफल के चार त्रिभुजों में बाँटते है।
View Solution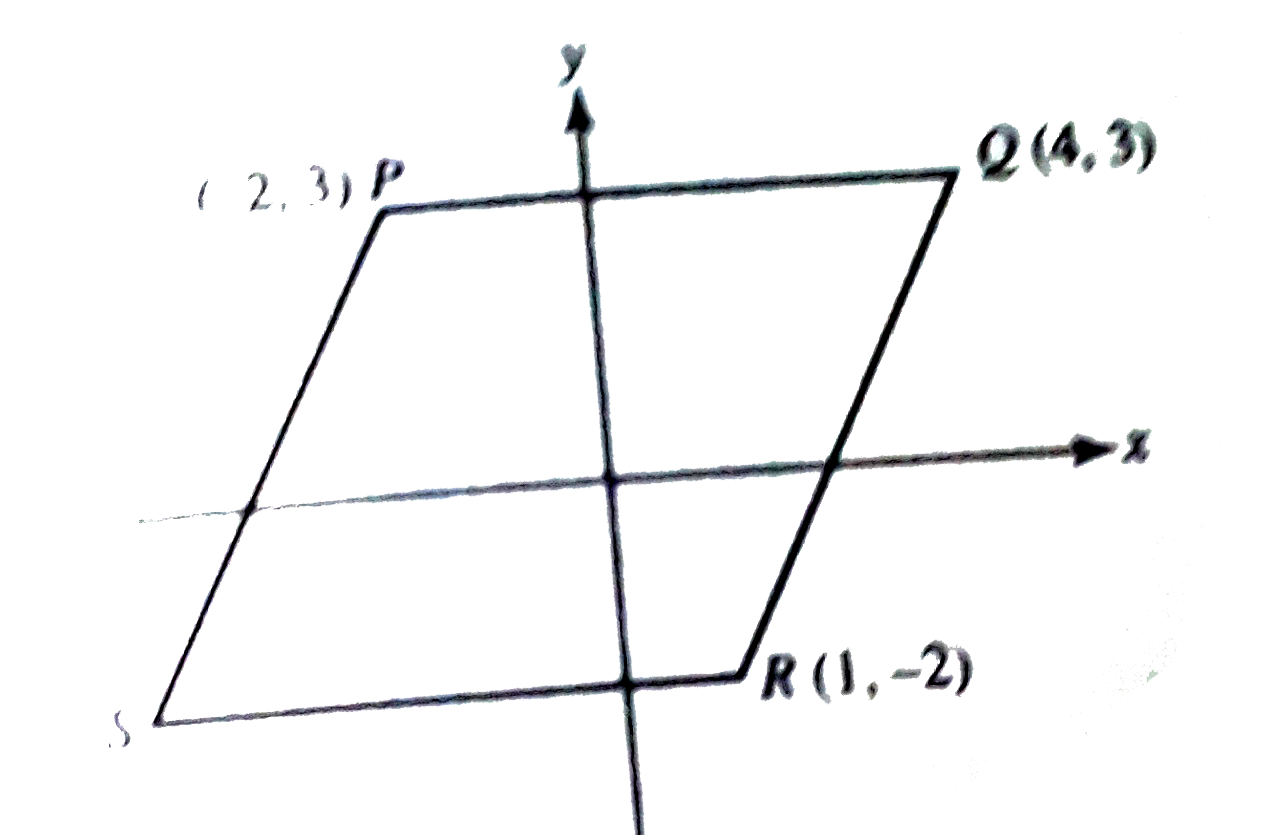
In the diagram above , PQRS is a parallelogram. What is the area of PQRS ?
View SolutionProve that two diagonals of a parallelogram divides it into four triangles of equal areas.
View SolutionProve that if each diagonal of a quadrilateral bisects it into two triangles of equal areas, then it is a parallelogram.
View SolutionProve that twice the area of a parallelogram is equal in the area of another parallelogram formed by taking as its adjacent sides of the diagonals of the former parallelogram.
View Solutionif parallelogram ABCD is congruent to parallelogram PQRS then (area(ABCD))/(area(PQRS)) =
View SolutionPQRS and ABRS are two parallelograms. X is a point on the shoulder of BR (PQRS) y || = (ABRS) y ||
View SolutionPQRS and ABRS are two parallelograms. X is a point on the shoulder of BR (/_\AXS) Y || = 1/2(PQRS) Why ||
View SolutionProve that A diagonal of a parallelogram divides it into two triangles of equal area.
View Solutionprove that the line segment joining the midpoints of two opposite sides of a parallelogram divides the parallelogram into two parallelograms with equal area.
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.

View Solution
