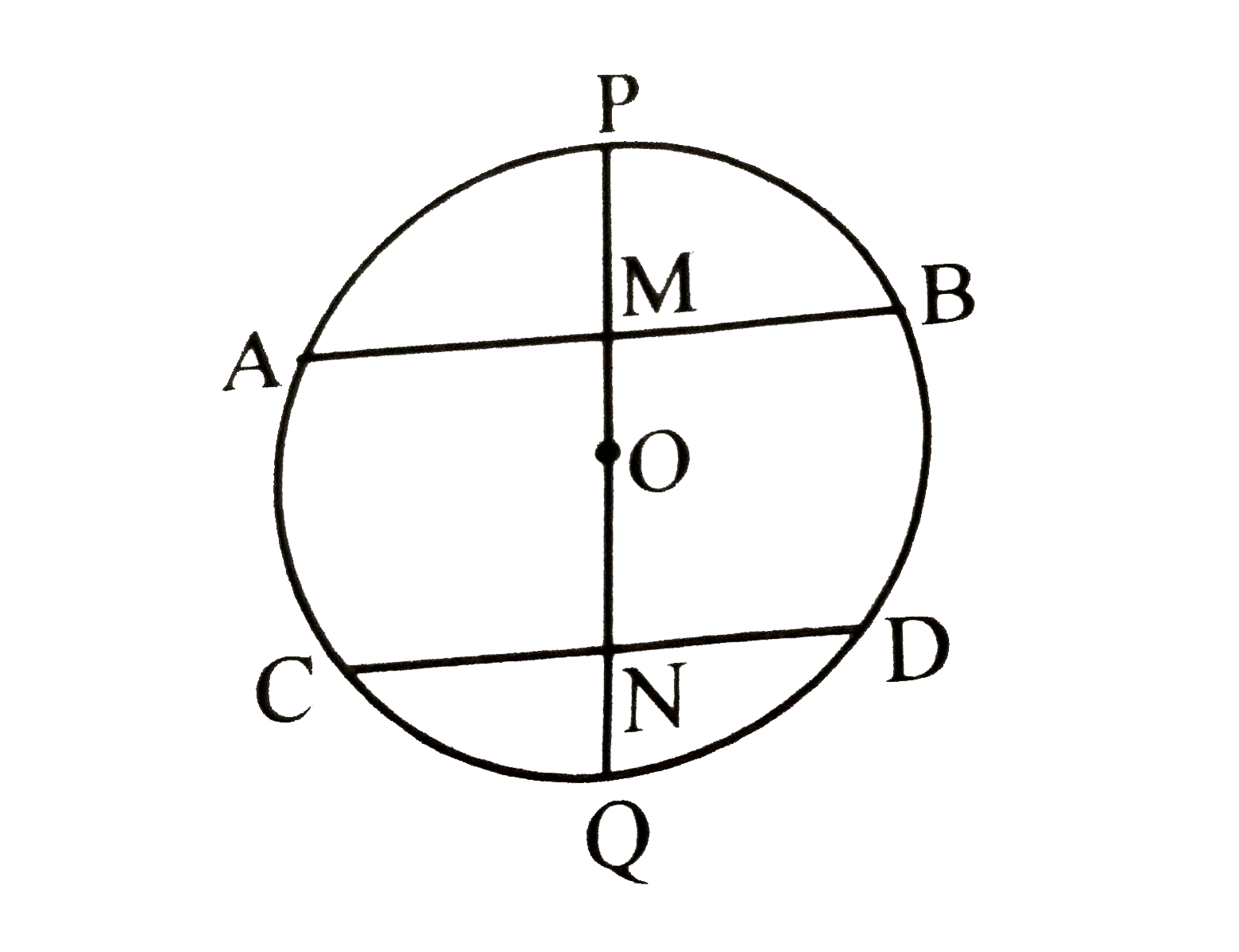
Prove that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
Video Solution
Text Solution
Given: PQ is a diameter of circle which bisects the chord AB at C
To prove: PQ bisects ∠AOB
Proof: In △BOC and △AOC
OA=OB (radius of the circle)
OC=OC (common)
AC=BC (given)
△AOC≅△BOC (By SSS)
So, ∠AOC=∠BOC (By CPCT)
∴ PQ bisects ∠AOB.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A chord of a circle is equal to its radius. The angle subtended by this chord at a point on the circumference is
A75∘B60∘C150∘D120∘ - Question 2 - Select One
If the length of a chord of a circle is equal to that of the radius of the circle , then the angle subtended , in radians , at the centre of the circle by the chord is
A1Bπ2Cπ3Dπ4 - Question 3 - Select One
If the chord of a circle is equal to the radius of the circle, then the angle subtended by the chord at a point on the minor arc is:
A120∘B150∘C100∘D110∘
A chord of a circle is equal to its radius. The angle subtended by this chord at a point on the circumference is
View SolutionProve that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
 View Solution
View SolutionIs every chord of a circle also a diameter?
View SolutionProve that a diameter AB of a circle bisects all those chords which are parallel to the tangent at the point A.
View SolutionLet p and q be the length of two chords of a circle which subtend angles 36∘and60∘ respectively at the centre of the circle . Then , the angle (in radian) subtended by the chord of length p + q at the centre of the circle is (use π=3.1 )
View Solution

