Prove that the area in the first quadrant enclosed by the axis, the line $x = \sqrt{3} y$ and the circle $x^{2} + y^{2} = 4 i s π / 3 .$

Video Solution

Text Solution

Verified by Experts

$x^{2} + y^{2} = 4$ is the equation of a circle whose centre is (0, 0) and radius is 2. On solving the equation of circle to the straight line $x = \sqrt{3} y$ we obtained the points of intersection $A (\sqrt{3}, 1)$ and $D (- \sqrt{3}, - 1)$ .

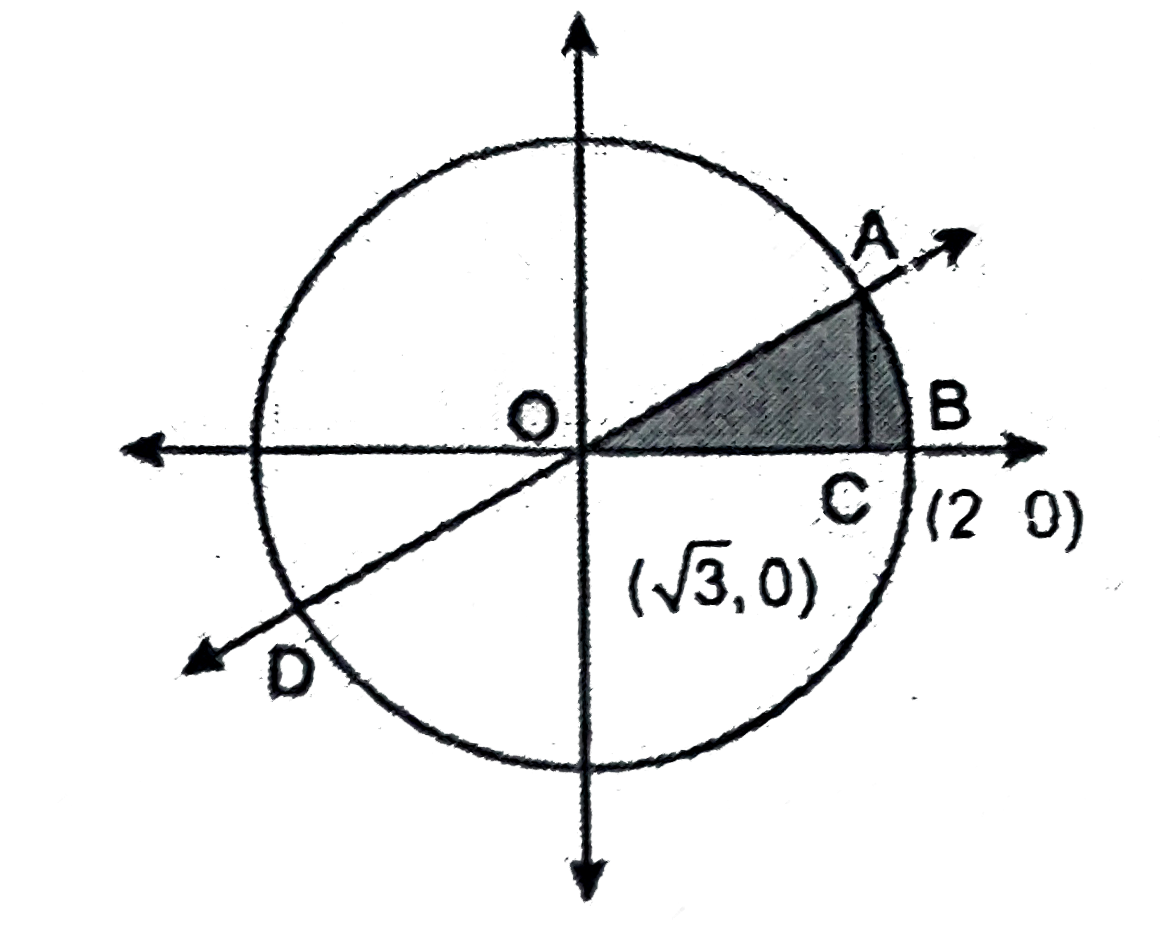
Now required area
$=$ area of OACO + area of CABC
$= \int_{0}^{\sqrt{3}} \frac{x}{\sqrt{3}} d x + \int_{\sqrt{3}}^{2} \sqrt{4 - x^{2}} d x$
$= {[\frac{x^{2}}{2 \sqrt{3}}]}_{0}^{\sqrt{3}} + {[\frac{x}{2} \sqrt{4 - x^{2}} + \frac{4}{2} {sin}^{- 1} \frac{x}{2}]}_{\sqrt{3}}^{- 1}$
$= \frac{\sqrt{3}}{2} + [(0 + 2 {sin}^{- 1} 1) - (\frac{\sqrt{3}}{2} + 2 {sin}^{- 1} \frac{\sqrt{3}}{2})]$
$= \frac{\sqrt{3}}{2} + 2 \cdot \frac{π}{2} - \frac{\sqrt{3}}{2} - 2 \cdot \frac{π}{3}$
$= \frac{π}{3}$ sq. units.

|

Updated on:21/07/2023

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF INTEGRALS-Exercise 8.1

Home
Ask Doubt
Profile