Prove that the centre of a circle touching two intersecting lines lies on the angle bisector of the lines.
To prove that the center of a circle touching two intersecting lines lies on the angle bisector of the lines, we can follow these steps:
1. Understand the Setup:
Let the two intersecting lines be denoted as RP and QP which intersect at point P. Let O be the center of the circle that touches both lines RP and QP at points R and Q respectively.
2. Identify Tangents:
Since O is the center of the circle, the segments OR and OQ are the radii of the circle. The tangents from a point to a circle are perpendicular to the radius at the point of tangency. Therefore, we have:
∠ORP=90∘and∠OQP=90∘
3. Establish Angles:
We need to prove that the angle ∠QPO is equal to ∠RPO. To do this, we will analyze triangles OQP and ORP.
4. Triangles Analysis:
In triangles OQP and ORP:
- OR=OQ (both are radii of the circle)
- OP is common to both triangles
- ∠ORP=90∘ and ∠OQP=90∘
5. Use RHS Congruence:
Since we have:
- One side equal (common side OP)
- One side equal (radii OR=OQ)
- Right angles ∠ORP=∠OQP=90∘
By the RHS (Right angle-Hypotenuse-Side) congruence criterion, we can conclude that:
△OQP≅△ORP
6. Corresponding Parts of Congruent Triangles (CPCT):
From the congruence of triangles, we can state that:
∠QPO=∠RPO
7. Conclusion:
Since ∠QPO=∠RPO, the line OP bisects the angle ∠RQP. Therefore, the center O lies on the angle bisector of the angle formed by the intersecting lines RP and QP.
Thus, we have proved that the center of the circle touching two intersecting lines lies on the angle bisector of the lines.
Let the two intersecting lines be denoted as RP and QP which intersect at point P. Let O be the center of the circle that touches both lines RP and QP at points R and Q respectively.
Since O is the center of the circle, the segments OR and OQ are the radii of the circle. The tangents from a point to a circle are perpendicular to the radius at the point of tangency. Therefore, we have:
∠ORP=90∘and∠OQP=90∘
We need to prove that the angle ∠QPO is equal to ∠RPO. To do this, we will analyze triangles OQP and ORP.
In triangles OQP and ORP:
- OR=OQ (both are radii of the circle)
- OP is common to both triangles
- ∠ORP=90∘ and ∠OQP=90∘
Since we have:
- One side equal (common side OP)
- One side equal (radii OR=OQ)
- Right angles ∠ORP=∠OQP=90∘
△OQP≅△ORP
From the congruence of triangles, we can state that:
∠QPO=∠RPO
Since ∠QPO=∠RPO, the line OP bisects the angle ∠RQP. Therefore, the center O lies on the angle bisector of the angle formed by the intersecting lines RP and QP.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS14videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CIRCLESEXERCISE - EXERCISE 9.2 VERY SHORT ANSWER TYPE QUESTIONS10videos
CIRCLES
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - Long Answer Type Questions10videos
ARITHMETIC PROGRESSIONS
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
Similar Questions
Find the locus of centres of circles which touch two intersecting lines.
View SolutionProve that the line of centres of two intersecting circles subtends equal angles at the two points of intersection
View SolutionThe locus of centre of the circle touching x-axis nad the line y=x is
View SolutionProve that two lines that are respectively perpendicular to two intersecting lines intersect each other .
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionTwo chords AB and AC of a circle are equal. Prove that the centre of the circle lies on the angle bisector of ∠BAC.
View SolutionProve that the line joining centres of two interesting circles subtends equal angles at the two points of intersection.
View SolutionProve that If the bisector of any angle of a triangle and the perpendicular bisector of its opposite side intersect, they will intersect on the circumcircle of the triangle.
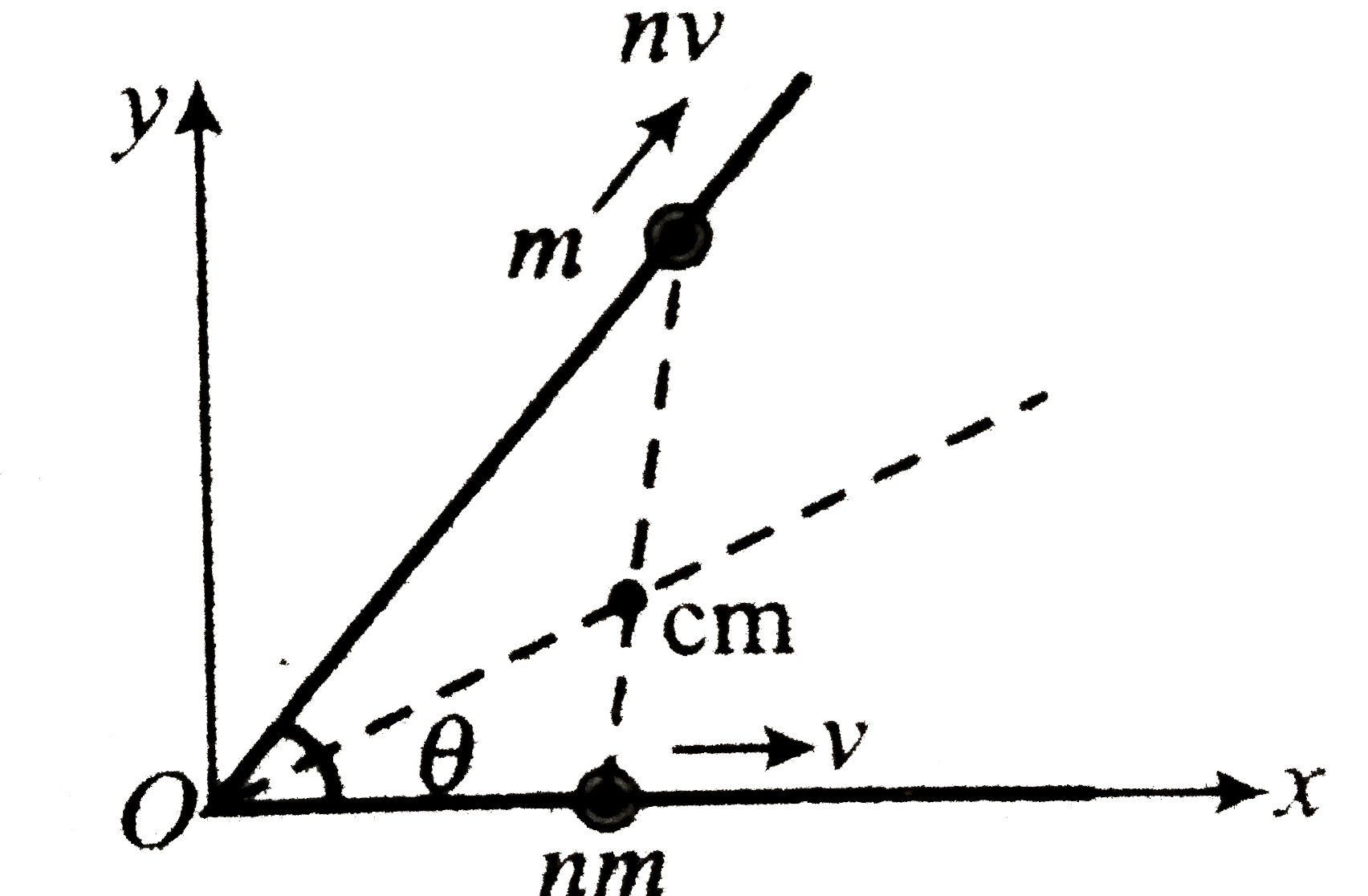
View SolutionTwo masses nm and m, start simultaneously from the intersection of two straight lines with velocities v and nv respectively. It is observed that the path of their centre of mass is a straight line bisecting the angle between the given straight lines. Find the magnitude of the velocity of centre of mass. [Here θ=angle between the lines]
 View Solution
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View Solution

