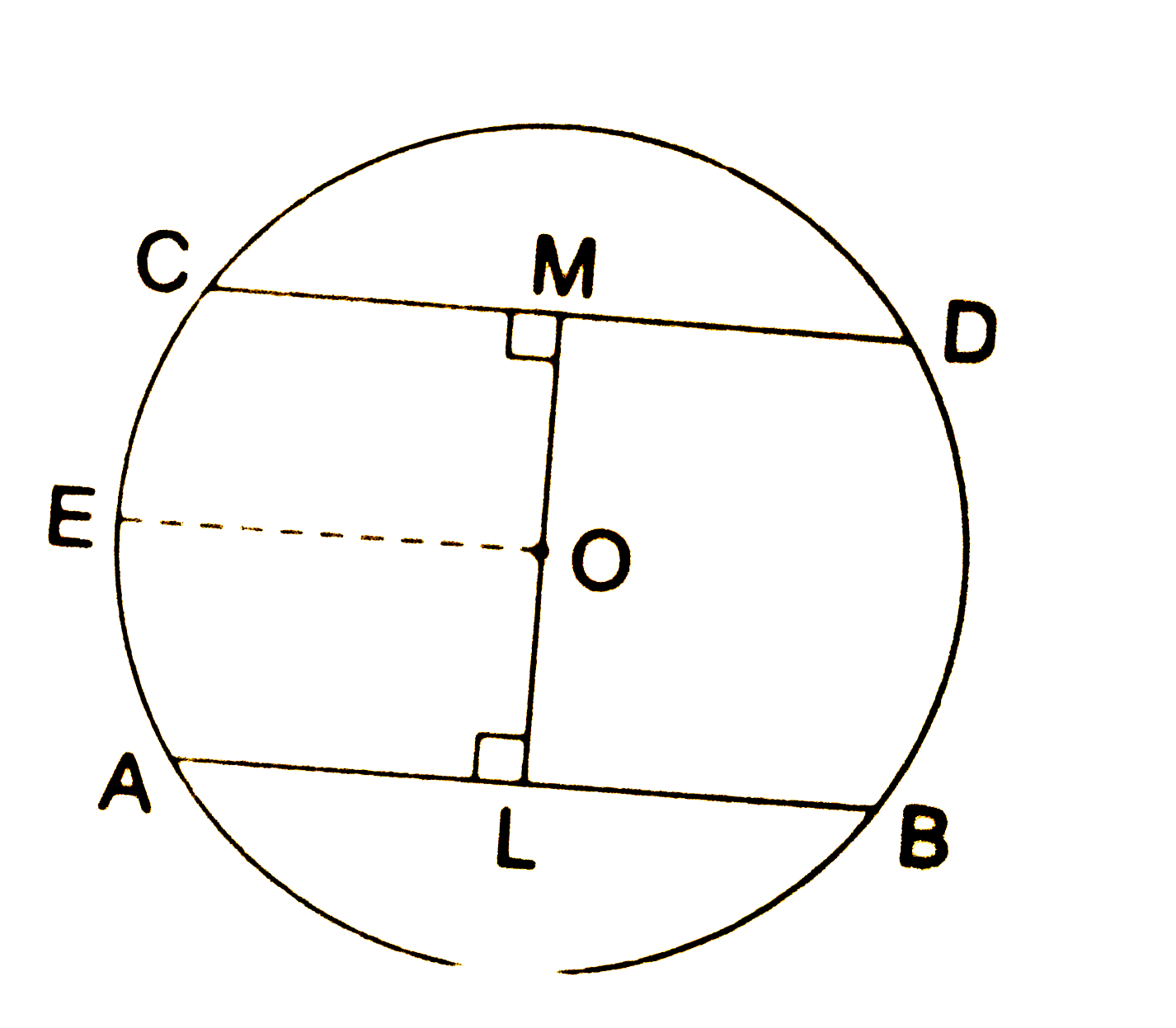
Prove that the line joining the mid-points of two parallel chords of a circle passes through the centre.
Given : L and M are midpoints of two parallel chords AB and CD respectively of a circle C(O,r) .
To prove : LOM is a straight line.
Construction : Join OL,OM and draw OE ∣∣ AB ∣∣ CD .
Proof : We know that the line joining the centre of a circle to the midpoint of a chord is perpendicular to the chord.
∴OL⊥AB and OM⊥OE
Now, OL⊥AB and AB∣∣OE⇒OL⊥OE
⇒∠EOL=90∘
OM⊥CD and CD∣∣OE⇒OM⊥OE
⇒∠EOM=90∘
∴∠EOL+∠EOM=180∘
Hence, LOM is a straight line.
Similar Questions
Knowledge Check
The chord of a circle which passes through the centre is___the radius
AThriceBDoubleCHalfDEqual to
Prove that the segment joining the point of contact of two parallel tangents passes through the centre.
View SolutionIf a line segment joining mid-points of two chords of a circle passes through the centre of the circle, prove that the two chords are parallel.
View SolutionProve that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
View SolutionProve that the line joining the mid-points of the two sides of a triangle is parallel to the third side.
View SolutionProve that the line joining the mid-points of the diagonals of a trapezium is parallel to the parallel sides of trapezium and is half of their difference.
View SolutionProve that the line segment joining the mid points of two side of a triangle is parallel to the third side and equal to half of it.
View SolutionThe line joining the mid-points of two sides of a triangle is parallel to the third side.
View Solution
