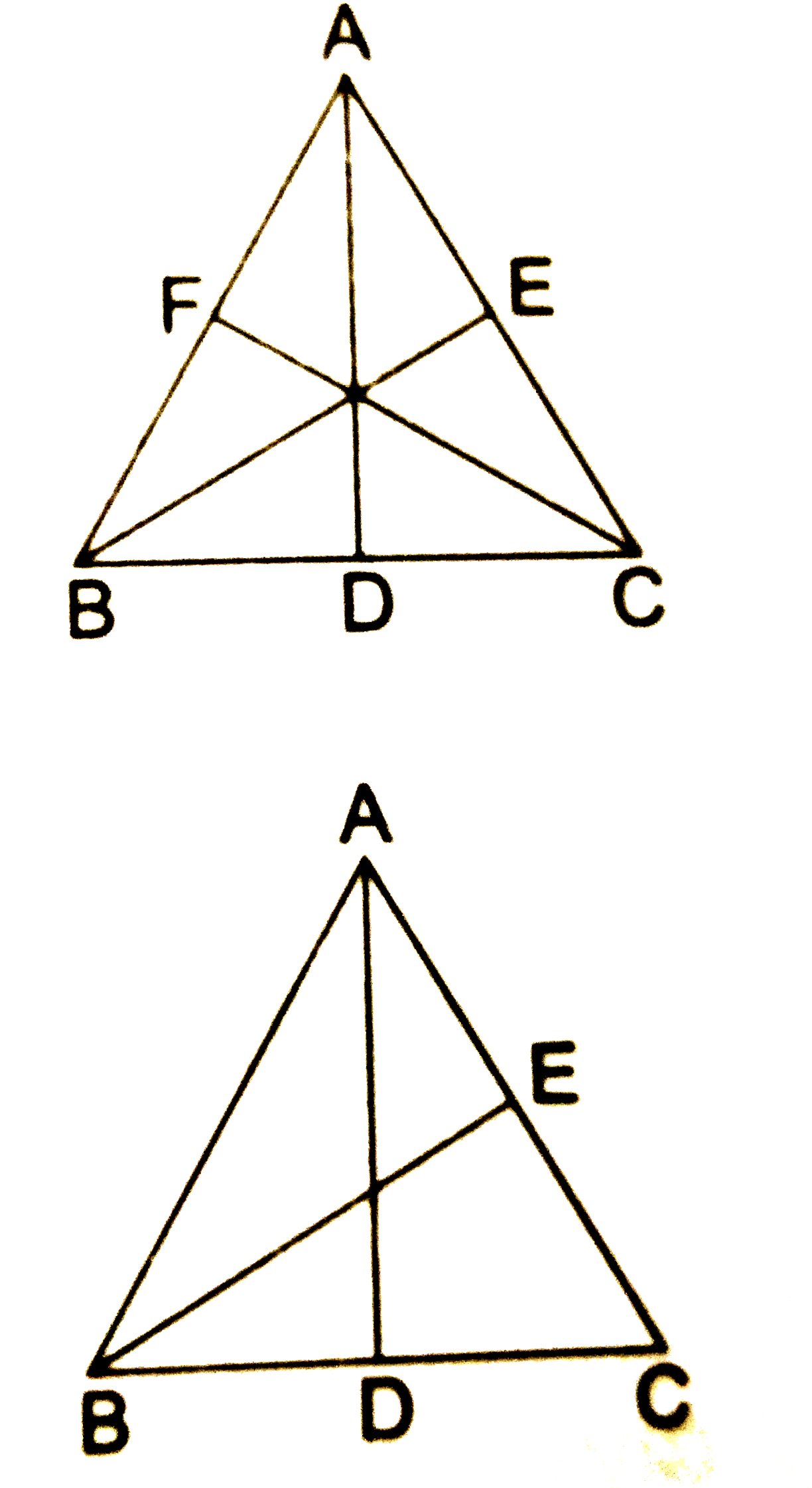
Prove that the medians of an equilateral triangle are equal.
GIVEN A ΔABC in which AB=BC=ACandAD,BE and CF are its medians.
TO PROVEV AD=BE=CF.
PROOF In ΔADCandΔBEA, we have
AC=BA (given),
DC=EA [∵BC=AC⇒12BC=12AC]
and ∠ACD=∠BAE [each equal to 60∘]
∴ ΔADC≅ΔBEA (SAS-criteria).
∴ AD=BE (c.p.c.t.).
Similarly, BE = CF.
Hence, AD = BE = CF.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Using the concept of slope, prove that medians of an equilateral triangle are perpendicular to the corresponding sides.
View SolutionProve that the area of an equilateral triangle is equal to √34a2, where a is the side of the triangle.
View SolutionProve that the area of an equilateral triangle is equal to √34a2, where a is the side of the triangle. GIVEN : An equilateral triangle ABC such that AB=BC=CA=a. TO PROVE : ar(ABC)=√34a2 CONSTRUCTION : Draw AD⊥BC.
View SolutionProve that a median of an equilateral triangle is perpendicular to the corresponding side.
View SolutionProve that the angle opposite to the equal sides of an equilateral triangle are equal.
View SolutionProve that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
View SolutionProve that the area of an equilateral triangle described on a side of a right-angled isosceles triangle is half the area of the equilateral triangle described on its hypotenuse.
View SolutionProve that each angle of an equilateral triangle is 600
View SolutionProve that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
View SolutionIf l is the length of the median of an equilateral triangle, then what is its area?
View Solution
